Обратная матрица и способы ее нахождения
Рассмотрим квадратную матрицу
A = 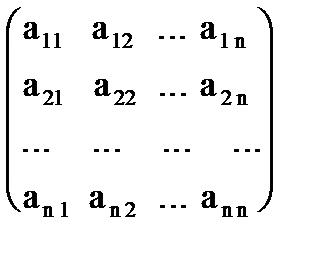 .
.
Обозначим ee определитель D =det (A).
Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля (D 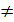 0), и вырожденной, или особенной, если определитель равен нулю (D = 0).
0), и вырожденной, или особенной, если определитель равен нулю (D = 0).
Квадратная матрица В называется обратной для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.
Теорема 1.2. Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.
Матрица, обратная для матрицы А, обозначается через А-1. Составим матрицу
A*= 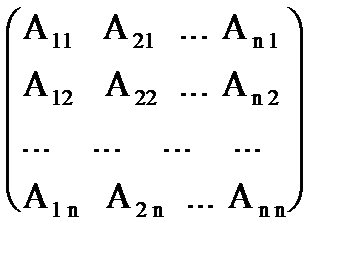 ,
,
где Аij - алгебраические дополнения элементов aij, причем каждое алгебраическое дополнение к элементу aij стоит на пересечении j–ой строки и i–ого столбца. Такая матрица называется присоединенной или взаимной.
Обратная матрица для А вычисляется по формуле
А-1 =  A*, (2.3)
A*, (2.3)
Т.е. для нахождения обратной матрицы надо найти присоединенную матрицу и все ее элементы разделить на определитель исходной
Вычисление обратной матрицы по формуле (2.3) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить обратную матрицу с помощью метода элементарных преобразований (ЭП).
Элементарными называются следующие преобразования матрицы:
1) перестановка двух любых строк (или столбцов),
2) умножение строки (или столбца) на отличное от нуля число,
3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Любую неособенную матрицу А путем элементарных преобразований только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А элементарные преобразования в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать элементарные преобразования над матрицами А и Е одновременно, записывая обе матрицы рядом через черту, но в процессе преобразований следует использовать только строки или только столбцы.
Пример 1.15. Для матрицы А = 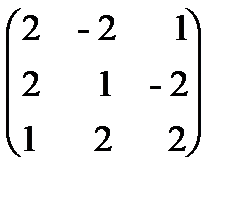 найти обратную.
найти обратную.
Решение. Находим сначала детерминант матрицы А
D = det А = 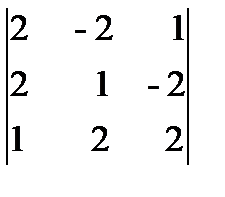 = 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D
= 27 ¹ 0, значит, обратная матрица существует и мы ее можем найти по формуле: А-1 = 1/D 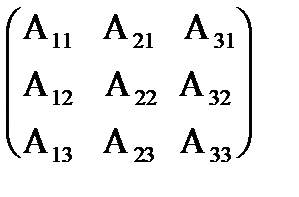 , где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем:
, где Аi j (i,j=1,2,3) - алгебраические дополнения элементов аi j исходной матрицы. Имеем: 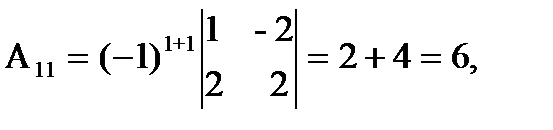
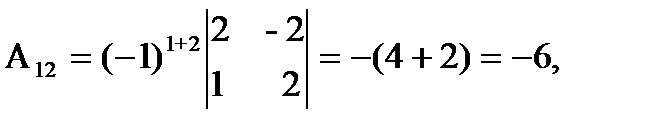
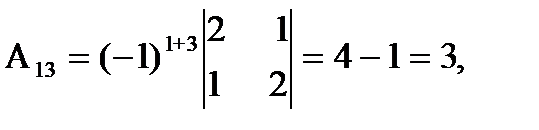
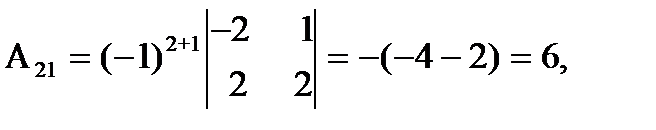
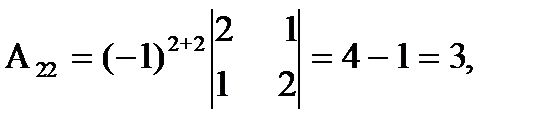
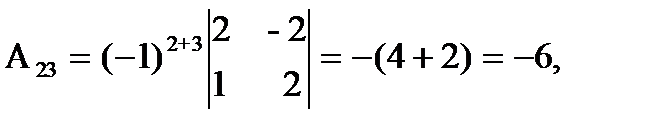
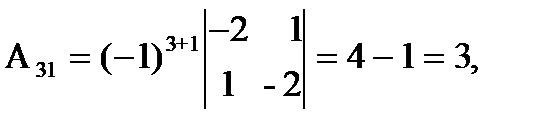
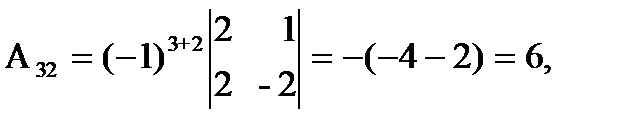
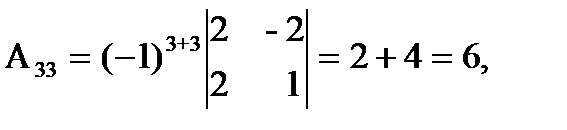 откуда
откуда
А-1 = 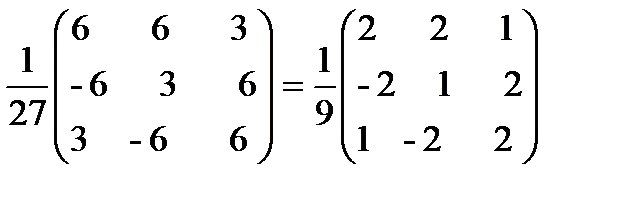 .
.
Проверим равенство АА-1=Е

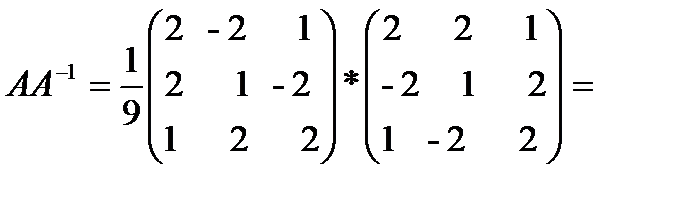
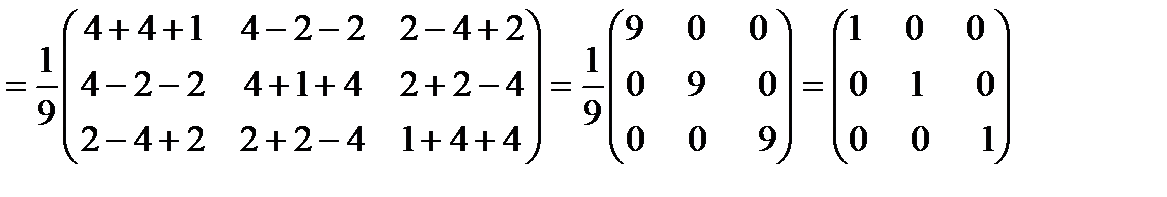
Пример 1.16. Методом элементарных преобразований найти обратную матрицу для матрицы: А= 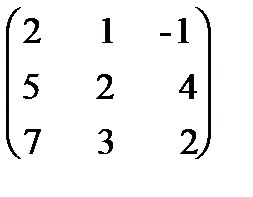 .
.
Решение.Приписываем к исходной матрице справа единичную матрицу того же порядка: 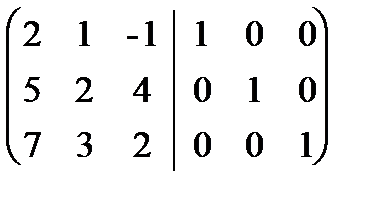 . С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей.
. С помощью элементарных преобразований столбцов приведем левую “половину” к единичной, совершая одновременно точно такие же преобразования над правой матрицей.
Для этого поменяем местами первый и второй столбцы: 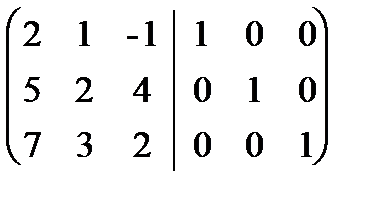 ~
~ 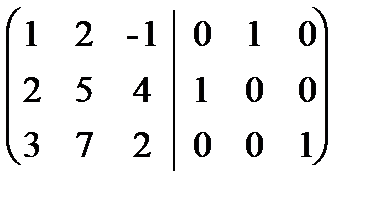 . К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2:
. К третьему столбцу прибавим первый, а ко второму - первый, умноженный на -2: 
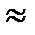
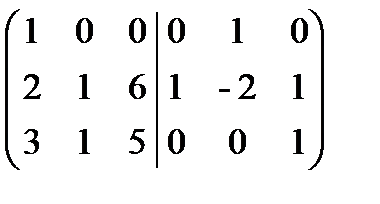 . Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй:
. Из первого столбца вычтем удвоенный второй, а из третьего - умноженный на 6 второй: 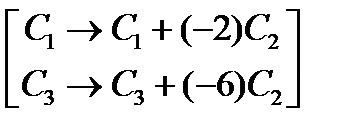
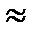
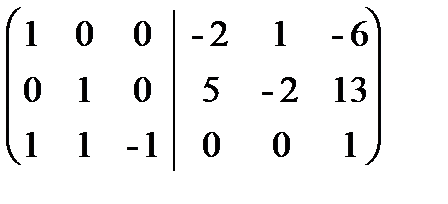 . Прибавим третий столбец к первому и второму:
. Прибавим третий столбец к первому и второму: 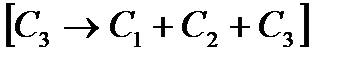
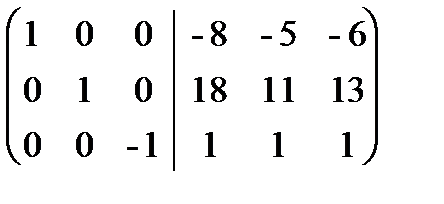 . Умножим последний столбец на -1:
. Умножим последний столбец на -1: 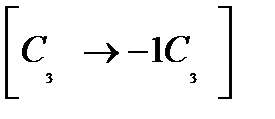
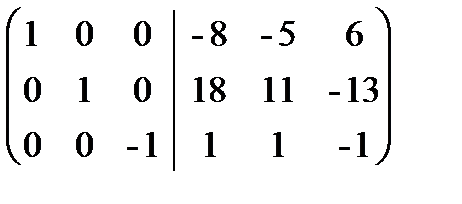 . Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
. Полученная справа от вертикальной черты квадратная матрица является обратной к данной матрице А. Итак,
А-1 = 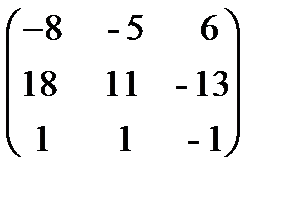 .
.
Сделаем проверку А-A-1-= 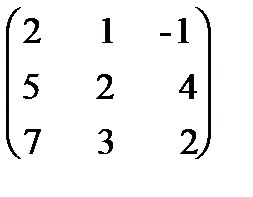
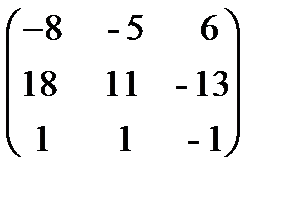 =
= 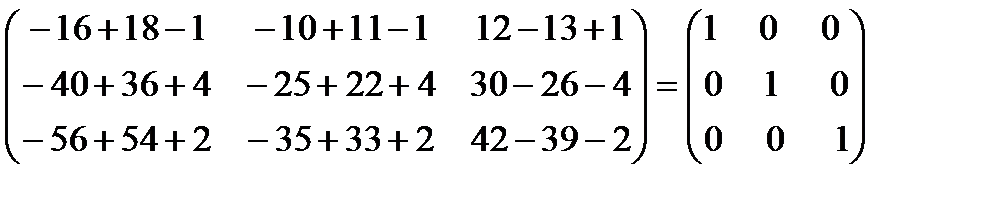 .
.
Дата добавления: 2015-09-29; просмотров: 1427;
