Виды матриц и их определители

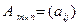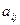Матрицей размерности называется таблица чисел , содержащая 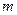строк и 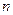столбцов. Числа 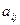называются элементами этой матрицы, где 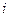– номер строки, 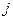– номер столбца, на пересечении которых стоит данный элемент. Матрица, содержащая 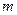строк и 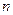столбцов, имеет вид: .

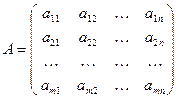Пример 1.1. Примером матрицы может служить таблица, представляющая собой данные по выпуску продукции молочного цеха в течение рабочей недели. В строках матрицы расположены данные по производству молока (в литрах), творога (в килограммах), сливочного масла (в килограммах), кефира (в литрах) соответственно. Столбцы отражают данные по дням недели от понедельника до субботы соответственно.

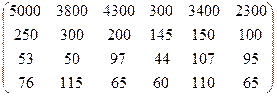
Виды матриц:

1) при 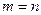– квадратная, в данном случае 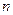называют порядком матрицы;

2) квадратная матрица, у которой все недиагональные элементы равны нулю

– диагональная;

3) диагональная матрица, у которой все диагональные элементы равны единице – единичная и обозначается ;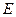

4) при 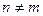– прямоугольная;

5) при 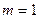– матрица-строка (вектор-строка);

6) при 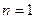– матрица-столбец (вектор-столбец);

7) при всех 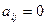– нулевая матрица.

Заметим, что основной числовой характеристикой квадратной матрицы является ее определитель. Определитель, соответствующий матрице 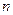-го по-

порядка, также имеет 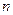-ый порядок.

Дадим ряд необходимых определений.

Определителем матрицы 1-го порядка называется число .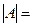

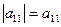Определителем матрицы 2-го порядка называется число 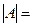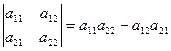. (1.1)

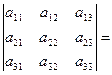
Определителем матрицы 3-го порядка называется число 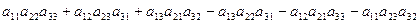. (1.2)

Минором М_ij элемента а_ij матрицы 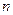-гопорядка А называется определитель матрицы 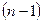-гопорядка, полученной из матрицыА путем вычеркивания i-ой строки и j-го столбца.

Алгебраическим дополнением А_ij элемента а_ij матрицы 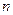-гопорядка Аназывается минор этого элемента, взятый со знаком .

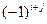Сформулируем основные свойства определителей, присущие определителям всех порядков и упрощающие их вычисление.

1. При транспонировании матрицы ее определитель не меняется.

2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак.

3. Определитель, имеющий две пропорциональные (равные) строки (столбца), равен нулю.

4. Общий множитель элементов какой-либо строки (столбца) определителя можно вынести за знак определителя.

5. Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если к элементам любой его строки (столбца) прибавить соответствующие элементы другой его строки (столбца), предварительно умноженные на любое число.

7. Определитель матрицы равен сумме произведений элементов любой его строки (столбца) на алгебраические дополнения этих элементов.

Поясним данное свойство на примере определителя 3-го порядка. В данном случае свойство 7 означает, что

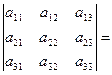
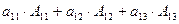(1.3)– разложение определителя по элементам 1-ой строки. Заметим, что для разложения выбирают ту строку (столбец), где есть нулевые элементы, так как соответствующие им слагаемые в разложении обращаются в ноль.

Свойство 7 представляет собой теорему о разложении определителя, сформулированную Лапласом.

8. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения соответствующих элементов другой его строки (столбца) равна нулю.

Последнее свойство часто называют псевдоразложением определителя.

Вопросы для самопроверки.

1. Что называется матрицей?

2. Какая матрица называется квадратной? Что понимается под ее порядком?

3. Какая матрица называется диагональной, единичной?

4. Какая матрица называется матрицей-строкой и матрицей-столбцом?

5. Что является основной числовой характеристикой квадратной матрицы?

6. Какое число называется определителем 1-го, 2-го и 3-го порядка?

7. Что называется минором и алгебраическим дополнением элемента матрицы?

8. Каковы основные свойства определителей?

9. С помощью какого свойства можно вычислить определитель любого порядка?