Виды матриц.
Матрица размера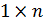 
, т.е. состоящая из одной строки называется вектор-строкой, а матрица размера 
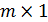, т.е. состоящая из одного столбца называется вектор-столбцом
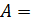
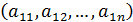- вектор-строка, 
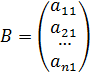- вектор-столбец.
Наряду с матрицей
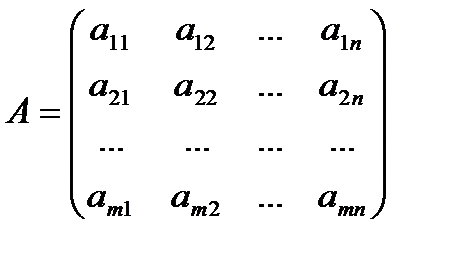
часто приходится рассматривать матрицу, столбцами которой являются строки матрицы 
(т.е. столбцы и строки меняются местами). Эта матрица называется транспонированной к 
и обозначается через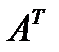 
:
.
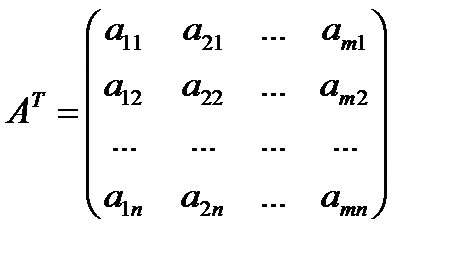Если матрица A имеет размер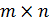 
, то транспонированная матрица AT имеет размер 
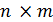. Заметим, что транспонированной матрицей к вектору-столбцу является вектор-строка, и наоборот:
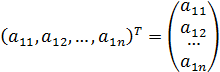
Если число строк матрицы равно числу ее столбцов, то матрица называется квадратной, а число 
ее строк (равное числу столбцов) – порядком квадратной матрицы.
Элементы квадратной матрицы 
такие, что i=j, называются диагональными. При этом диагональ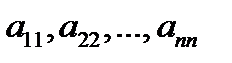 
квадратной матрицы называется главной диагональю, а диагональ 
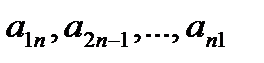– побочной диагональю.
Квадратная матрица называется треугольной, если все ее элементы, которые находятся ниже (или выше) главной диагонали, равны нулю, т.е. треугольная матрица имеет вид
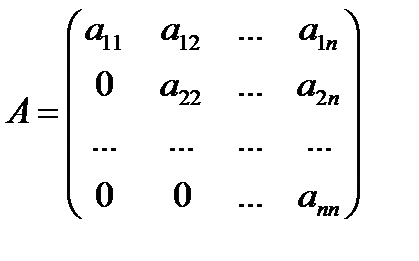или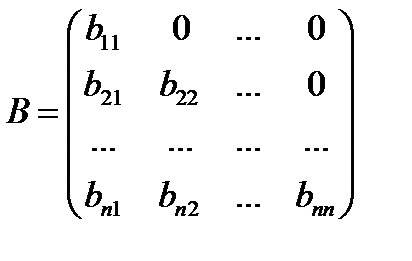 
.
При этом матрицу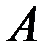 
называют верхнетреугольной, а матрицу 
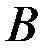– нижнетреугольной.
Квадратная матрица, у которой все внедиагональные элементы равны нулю, называется диагональной, например
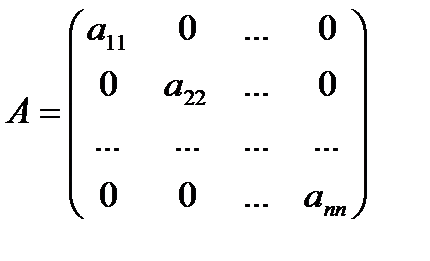
Диагональная матрица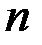 
-го порядка, у которой все диагональные элементы равны единице называется единичной матрицей и обозначается E
.
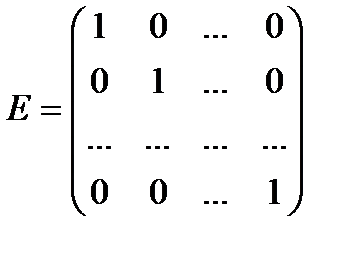Легко проверить, что для любой матрицы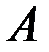 
-го порядка имеют место равенства
.
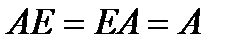Матрица любого размера называется нулевой, если все ее элементы равны нулю
.
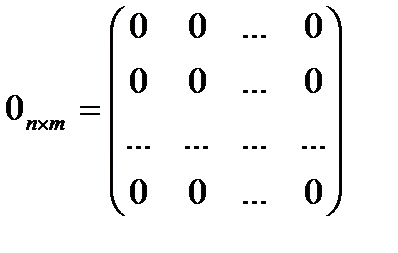Дата добавления: 2015-09-29; просмотров: 965;