Ранние и поздние сроки свершения событий. Резерв времени событий

Все пути, отличные по продолжительности от критического, располагают резервами времени. Разность между длиной критического пути и любого некритического называется полным резервом времени данного некритического пути и обозначается : .

Ранним сроком свершения события называется самый ранний момент времени, к которому завершаются все предшествующие этому событию работы, т.е. определяется продолжительностью максимального пути, предшествующего событию , т.е.:

или

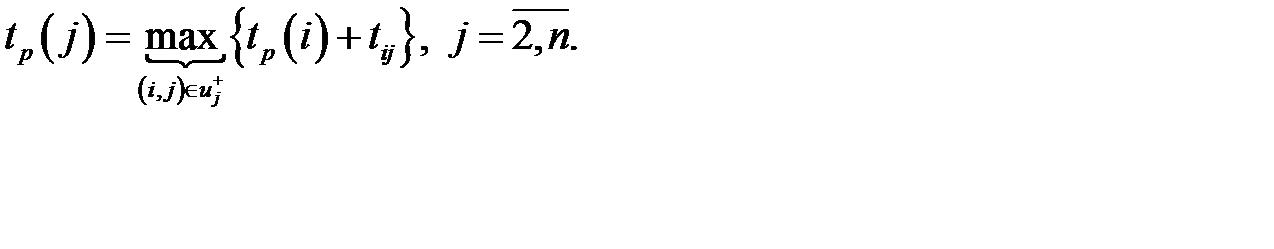
Чтобы найти ранний срок совершения события j , нужно знать критический путь ориентированного подграфа, состоящего из множества путей, пред шествующих данному событию j . Ранний срок исходного события равен нулю: t_p(1)=0.

Поздним сроком совершения события называется самый поздний момент времени, после которого остается ровно столько времени, сколько необходимо для завершения всех работ, следующих за этим событием. Самый поздний из допустимых сроков свершения события в сумме с продолжительностью выполнения всех последующих работ должен не превышать длины критического пути. Поздний срок свершения события вычисляется как разность между продолжительностью критического пути и продолжительностью максимального из последующих за событием путей

:

или

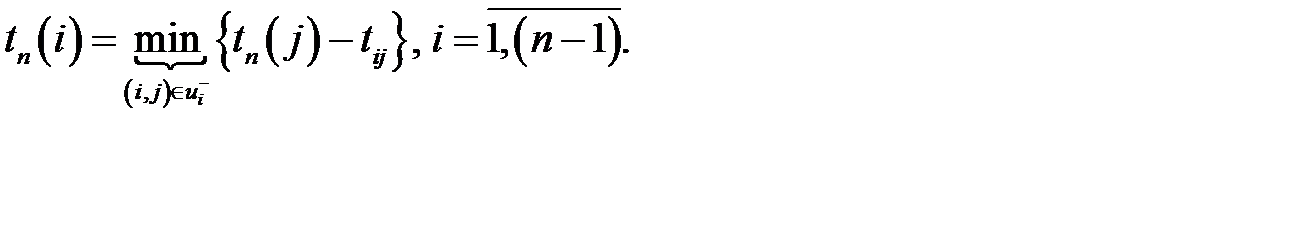
Для событий, лежащих на критическом пути, ранний и поздний сроки свершения этих событий совпадают .

Разность между поздним и ранним сроками свершения события составляет резерв времени события : . Интервал называется интервалом свободы события . Резерв времени события показывает максимально допустимое время, на которое можно отодвинуть момент его свершения, не увеличивая критический путь. Так как сумма определяет продолжительность пути максимальной длины, проходящего через это событие, то , т.е. резерв времени любого события равен полному резерву времени максимального пути, проходящего через это событие .

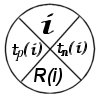При расчете временных параметров вручную удобно пользоваться четырехсекторным способом. При этом способе кружок сетевого графика, обозначающий событие, делится на четыре сектора. В верхнем секторе ставится номер события; в левом – наиболее раннее из возможных время свершения события ( ); в правом – наиболее позднее из допустимых время свершения события ; в нижнем секторе – резерв времени данного события : .

Для вычисления раннего срока свершения событий: , применяем формулу , рассматривая события в порядке возрастания номеров, от начального к завершающему, по входящим в это событие работам. Поздний срок свершения событий вычисляем по формуле , начиная с конечного события, для которого ( - номер конечного события), по выходящим из него работам.

Критические события имеют резерв времени равный нулю. Они и определяют критические работы и критический путь.

Пример 14.1. Пусть задан сетевой график, изображенный на рисунок 14.2.

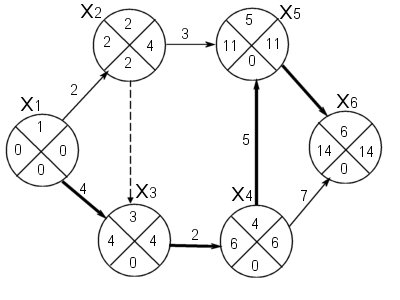
Рисунок 14.2

Решение. Вычислим ранние сроки свершения событий :

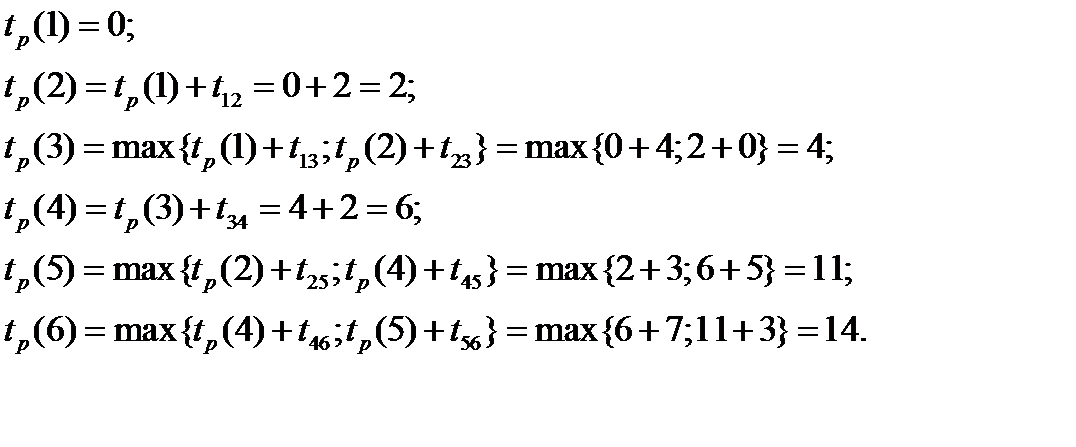
Итак, завершающее событие может произойти лишь на 14-ый день от начала выполнения проекта. Это максимальное время, за которое могут быть выполнены все работы проекта. Оно определяется самым длинным путем. Ранний срок свершения работы 6 =14 совпадает с критическим временем _кр - суммарной продолжительностью работ, лежащих на критическом пути. Теперь можно выделить работы, принадлежащие критическому пути, возвращаясь от завершающего события к исходному. Из двух работ, входящих в событие 6 , , длина критического пути определила работы (5, 6), так как ( ₅+ ₅₆)=14. Поэтому работа (5, 6) – критическая и т.д. Работы (1, 3), (3, 4), (4, 5), (5, 6) определили критический путь: _кр = (1-3-4-5-6).

Вычислим теперь поздние сроки свершения событий . Положим . Воспользуемся методом динамического программирования. Все расчеты будем вести от завершающего события к начальному событию. Поздние сроки свершения событий равны:

, так как после события 5 для завершения проекта нужно выполнить работу (5, 6) длительностью 3 дня. Из события 4 выходят две работы, поэтому:

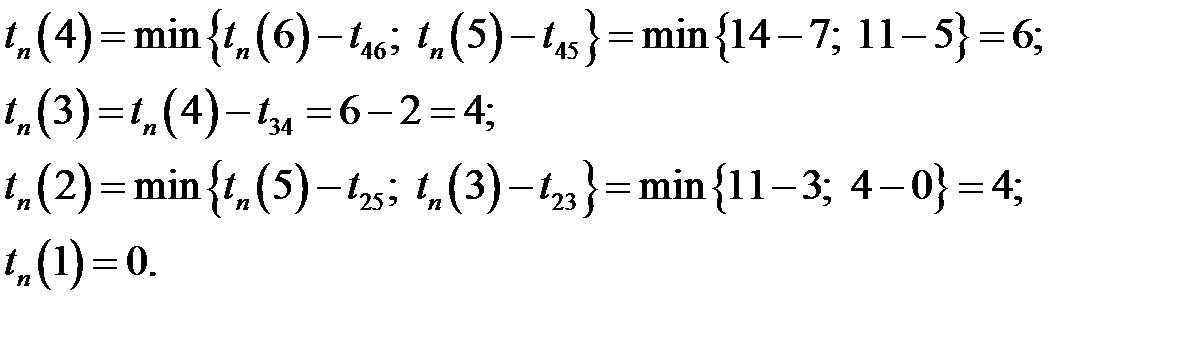
Резерв времени для события 2 равен: . Резервы остальных событий равны нулю, так как эти события критические.