Оптимизация проекта по ресурсам
Предположим, что проект задан сетевым графиком  и имеется количество ресурсов равное
и имеется количество ресурсов равное  . Каждая работа проекта характеризуется продолжительностью выполнения
. Каждая работа проекта характеризуется продолжительностью выполнения  и интенсивностью потребления ресурса
и интенсивностью потребления ресурса  . Под интенсивностью потребления будем понимать требуемое количество ресурса для выполнения работы
. Под интенсивностью потребления будем понимать требуемое количество ресурса для выполнения работы  в единицу времени. Рассмотрим случай, когда интенсивности постоянные, используются ресурсы одного вида и работы не допускают перерыва в выполнении.
в единицу времени. Рассмотрим случай, когда интенсивности постоянные, используются ресурсы одного вида и работы не допускают перерыва в выполнении.
Под оптимальным распределением ресурсов будем понимать такое размещение работ во времени, которое при заданной интенсивности потребления ресурсов обеспечило бы выполнение проекта в минимальный срок. На практике получили широкое применение эвристические методы распределения ресурсов, хотя они не всегда позволяют найти оптимальное решение. Сущность этих методов состоит в следующем.
1. Для каждой работы определяются ее ранние и поздние сроки начала и окончания и полные резервы времени: 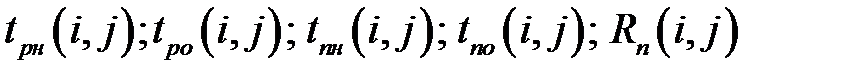 .
.
2. Строится сетевой график в календарной шкале времени по ранним срокам начала и окончания работ. По этапу ресурса выясняется интенсивность его потребления для каждого интервала времени.
П р е д в а р и т е л ь н ы й ш а г. Составляем линейный график Ганта выполнения проекта. На диаграмме каждая работа (i,j) изображается горизонтальным отрезком, длина которого в соответствующем масштабе равна времени ее выполнения. Начало каждой операции совпадает с ожидаемым сроком свершения ее начального события. Определяем по диаграмме критическое время tкр и критический путь.
П е р в ы й ш а г. 1. Проектируем на ось времени начало и конец каждой работы и обозначаем проекцию, совпадающую с началом координат -  , а следующую за ней -
, а следующую за ней -  .
.
2. Определяем полные резервы времени Rn  работ, расположенных над промежутком
работ, расположенных над промежутком  . Нумеруем эти работы в порядке возрастания их полных резервов. Работы с одинаковыми полными резервами времени нумеруем в порядке убывания интенсивностей потребления ресурсов.
. Нумеруем эти работы в порядке возрастания их полных резервов. Работы с одинаковыми полными резервами времени нумеруем в порядке убывания интенсивностей потребления ресурсов.
3. Суммируем последовательно интенсивности работ, расположенных над промежутком  в порядке возрастания присвоенных им номеров, и сравниваем полученные суммы с заданной величиной ресурсов R. Все работы, сумма интенсивностей которых не превосходит R, оставляем в первоначальном положении. Если после прибавления интенсивности какой-нибудь работы окажется, что суммарное потребление ресурсов больше R, то эту работу сдвигаем вправо на величину рассматриваемого промежутка, и переходим к добавлению интенсивности следующей работы и так продолжаем до тех пор, пока не будут рассмотрены все работы, расположенные над промежутком
в порядке возрастания присвоенных им номеров, и сравниваем полученные суммы с заданной величиной ресурсов R. Все работы, сумма интенсивностей которых не превосходит R, оставляем в первоначальном положении. Если после прибавления интенсивности какой-нибудь работы окажется, что суммарное потребление ресурсов больше R, то эту работу сдвигаем вправо на величину рассматриваемого промежутка, и переходим к добавлению интенсивности следующей работы и так продолжаем до тех пор, пока не будут рассмотрены все работы, расположенные над промежутком  .
.
Результатом выполнения этого действия является новая линейная диаграмма, момент  которой считаем началом оставшейся части комплекса работ. Работы
которой считаем началом оставшейся части комплекса работ. Работы  , расположенные над промежутком
, расположенные над промежутком  , изображаем так, чтобы их начала совпадали с новыми ранними сроками свершения событий.
, изображаем так, чтобы их начала совпадали с новыми ранними сроками свершения событий.
О б щ и й ш а г. Предположим, что выполнено k шагов алгоритма и получен линейный график, момент  которого является началом оставшейся части работ проекта.
которого является началом оставшейся части работ проекта.
1. Проектируем на ось времени начало и конец каждой работы, рассмотренной над промежутком  , и обозначаем проекцию, ближайшую к
, и обозначаем проекцию, ближайшую к  , через
, через  . Так выделяем новый промежуток
. Так выделяем новый промежуток  .
.
2. Определяем полные резервы работ  , расположенных над промежутком
, расположенных над промежутком  и номеруем их. Сначала нумеруем работы
и номеруем их. Сначала нумеруем работы  , начатые левее момента
, начатые левее момента  , согласно возрастанию разностей между полными резервами этих работ и длительностями от начала до момента
, согласно возрастанию разностей между полными резервами этих работ и длительностями от начала до момента  (длительности работ обозначим
(длительности работ обозначим  ). Работы с одинаковыми разностями нумеруем в порядке убывания интенсивностей. Все остальные работы нумеруем в порядке возрастания их полных резервов, а с одинаковыми резервами - в порядке убывания интенсивностей.
). Работы с одинаковыми разностями нумеруем в порядке убывания интенсивностей. Все остальные работы нумеруем в порядке возрастания их полных резервов, а с одинаковыми резервами - в порядке убывания интенсивностей.
3. Это действие выполняется так же, как и действие 3 первого шага. Однако следует иметь в виду, что если сдвигу подлежит работа  , начатая левее
, начатая левее  , то сдвигаем всю работу, т.е. начало этой работы устанавливаем в момент
, то сдвигаем всю работу, т.е. начало этой работы устанавливаем в момент  .
.
4. Проверяем, все ли работы проекта рассмотрены. Если все, то решение закончено; если нет, то возвращаемся к п.1 общего повторяющегося шага.
Пример 15.4.Пусть на промышленном предприятии составлен сетевой график выполнения работ. На его дугах, исходя из трудоемкости выполнения каждой работы, проставлены их продолжительность и необходимое число исполнителей.
Известно, что в распоряжении руководителей работ имеется 30 человек. Требуется распределить трудовые ресурсы во времени, т.е. определить сроки начала и окончания работ так, чтобы с имеющимися трудовыми ресурсами выполнить работы в минимальный срок, равный критическому пути для графика: tкр=16.
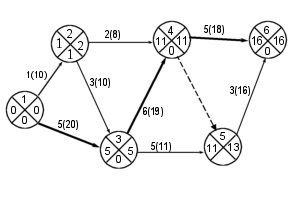
Рисунок 15.4
Решение. П р е д в а р и т е л ь н ы й ш а г. Расчет временных параметров сетевого графика по четырехсекторной схеме.
Критический путь: 1 – 3 – 4 - 6, tкр=16. Используя формулы,
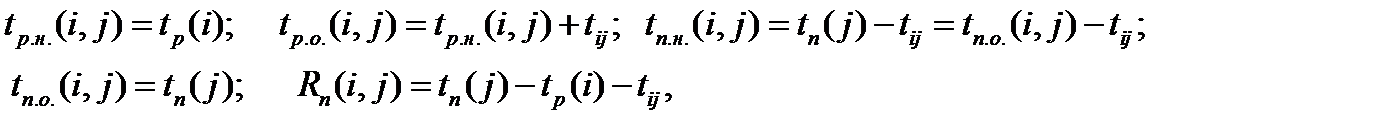
находим их значения.
Результаты расчетов сведем в таблицу:
| № | (  ) )
| 
| 
| 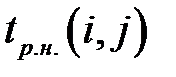
| 
| 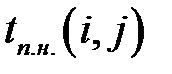
| 
| 
|
| (1, 2) | ||||||||
| (1, 3) | ||||||||
| (2, 3) | ||||||||
| (2, 4) | ||||||||
| (3, 4) | ||||||||
| (3, 5) | ||||||||
| (4, 5) | ||||||||
| (4, 6) | ||||||||
| (5, 6) |
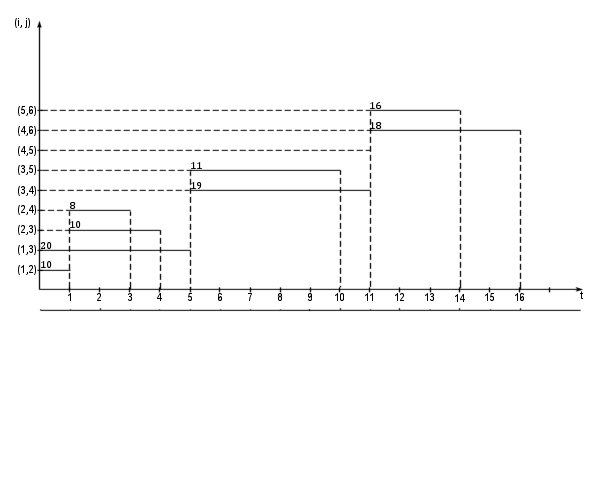
Построим линейный график Ганта (рисунок 15.5, а) по ранним срокам начала и окончания работ: начало каждой работы совпадает с ожидаемым сроком свершения ее начального события. Над горизонтальными отрезками написано число исполнителей работы.
Строим эпюру интенсивности потребления без учета его ограниченности (рисунок 15.5, б). Найдем на диаграмме критический путь: работа (4,6) заканчивается позже всех, через 16 дней после начала выполнения проекта. Следовательно, она критическая и  = 16. Работа (4,6) начинается в момент
= 16. Работа (4,6) начинается в момент  11. Находим работы с конечным событием (4), которые заканчиваются в это же время. Имеется только одна такая работа (3,4). Следовательно, она критическая. Работе (3,4) предшествует критическая работа (1,3). Таким образом,
11. Находим работы с конечным событием (4), которые заканчиваются в это же время. Имеется только одна такая работа (3,4). Следовательно, она критическая. Работе (3,4) предшествует критическая работа (1,3). Таким образом,  =(1 – 3 – 4 – 6).
=(1 – 3 – 4 – 6).
  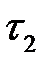 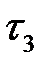 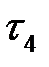 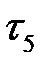 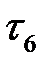 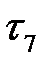 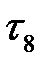
|
Рисунок 15.5, 
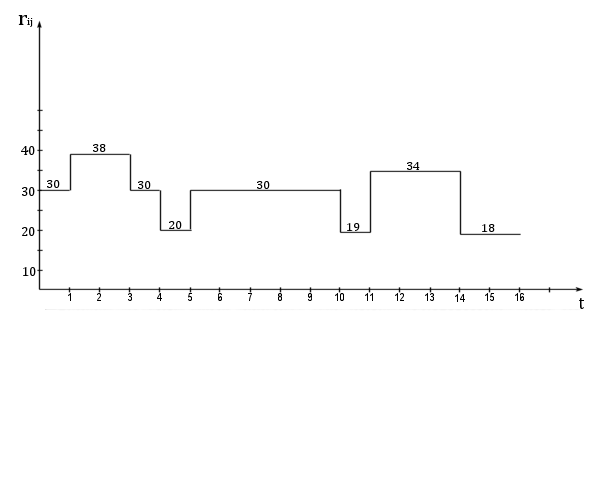
Рисунок 15.5, 
П е р в ы й ш а г.
1. Проектируем на ось времени t начала и окончания каждой работы. Определяем  и
и  (следующая проекция).
(следующая проекция).
2. Над промежутком  расположены работы (1, 2) и (1, 3). Так как сумма ресурсов для их выполнения 10+20=30 не превышает наличных ресурсов в 30 человек, то оставляем их в первоначальном положении. Так как
расположены работы (1, 2) и (1, 3). Так как сумма ресурсов для их выполнения 10+20=30 не превышает наличных ресурсов в 30 человек, то оставляем их в первоначальном положении. Так как  =20 >
=20 >  > 10, то работе (1, 3) присваиваем номер 1, а работе (1, 2) номер 2.
> 10, то работе (1, 3) присваиваем номер 1, а работе (1, 2) номер 2.
3. Анализируем промежуток  = (1, 3). Над ним работы (1,3), (2,3) и (2, 4). Сумма интенсивностей ресурсов 20 + 10 + 8 = 38 больше наличного ресурса в 30 единиц. Присваиваем номера работам. В первую очередь выполняются работы, начатые в промежутке
= (1, 3). Над ним работы (1,3), (2,3) и (2, 4). Сумма интенсивностей ресурсов 20 + 10 + 8 = 38 больше наличного ресурса в 30 единиц. Присваиваем номера работам. В первую очередь выполняются работы, начатые в промежутке  = (0, 1) – это работа (1, 3).
= (0, 1) – это работа (1, 3).
Ее интенсивность  = 20. Оставшиеся работы (2, 3) и (2, 4) упорядочим согласно возрастанию их полных резервов времени Rn(i,j): Rn(2, 3) = 1, Rn(2, 4) = 8. Следовательно, в момент
= 20. Оставшиеся работы (2, 3) и (2, 4) упорядочим согласно возрастанию их полных резервов времени Rn(i,j): Rn(2, 3) = 1, Rn(2, 4) = 8. Следовательно, в момент  = 1 начинаем выполнять работу (2, 3):
= 1 начинаем выполнять работу (2, 3):  + +
+ +  = 20 + 10 = 30, и присвоим ей номер 3. Начало работы (2, 4) сдвигаем к моменту
= 20 + 10 = 30, и присвоим ей номер 3. Начало работы (2, 4) сдвигаем к моменту  = 3 . Результаты сдвига отражены на новой линейной диаграмме (рисунок 15.6).
= 3 . Результаты сдвига отражены на новой линейной диаграмме (рисунок 15.6).
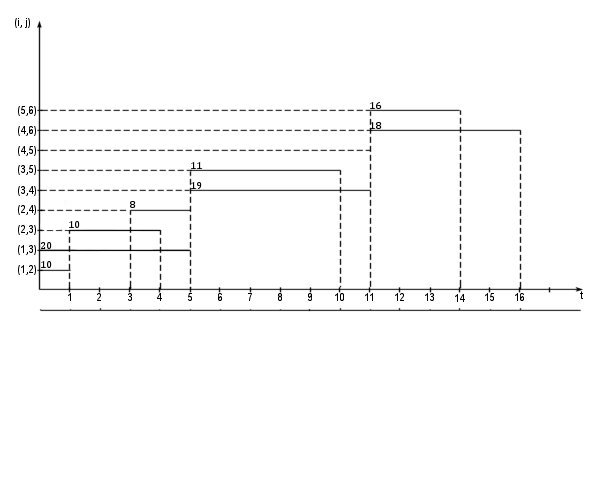





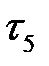
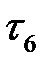
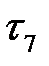
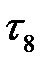
Рисунок 15.6
4. Сдвинув работу (2, 4) к моменту  = 3, замечаем, что в промежутке
= 3, замечаем, что в промежутке  = (3, 4) интенсивность потребления ресурса
= (3, 4) интенсивность потребления ресурса  = 38 > 30 превышает наличный ресурс в 30 единиц. Так как работы (1,3) и (2,3) начаты в предыдущих промежутках, то работу (2, 4) сдвигаем до момента
= 38 > 30 превышает наличный ресурс в 30 единиц. Так как работы (1,3) и (2,3) начаты в предыдущих промежутках, то работу (2, 4) сдвигаем до момента  = 4. В результате сдвига получаем новую линейную диаграмму (рисунок 15.7).
= 4. В результате сдвига получаем новую линейную диаграмму (рисунок 15.7).
5. Начало нового промежутка совпадает с началом работы (2, 4), конец - с окончанием работы (1, 3). В промежутке  = (4, 5) интенсивность потребления ресурса
= (4, 5) интенсивность потребления ресурса  = 20+8 = 28 < 30. Следовательно, работе (2,4) присваиваем номер 4.
= 20+8 = 28 < 30. Следовательно, работе (2,4) присваиваем номер 4.
6. Начало нового промежутка совпадает с  = 5, а конец
= 5, а конец  = 6. При
= 6. При  = 5 заканчивается работа (1,3) и начинаются работы (3,4) и (3,5). При
= 5 заканчивается работа (1,3) и начинаются работы (3,4) и (3,5). При  = 6 заканчивается работа (2, 4).
= 6 заканчивается работа (2, 4).
В промежутке  = (5, 6) интенсивность потребления ресурса превышает наличный запас ресурса:
= (5, 6) интенсивность потребления ресурса превышает наличный запас ресурса:  = 8+19+11 = 38 > 30. Так как работа (2, 4) начата в предыдущем промежутке, то выполнению в начале промежутка подлежат работы (3, 4) и (3,5). Их резервы времени: Rn(3, 4) = 0, Rn(3, 5) = 3. Следовательно, в момент
= 8+19+11 = 38 > 30. Так как работа (2, 4) начата в предыдущем промежутке, то выполнению в начале промежутка подлежат работы (3, 4) и (3,5). Их резервы времени: Rn(3, 4) = 0, Rn(3, 5) = 3. Следовательно, в момент  = 5 нужно начать работу (3, 4). Ей присваиваем номер 5. Начало работы (3, 5) сдвигаем к моменту
= 5 нужно начать работу (3, 4). Ей присваиваем номер 5. Начало работы (3, 5) сдвигаем к моменту  = 6. Результаты сдвига отображаем на новой линейной диаграмме, рисунок 15.8.
= 6. Результаты сдвига отображаем на новой линейной диаграмме, рисунок 15.8.
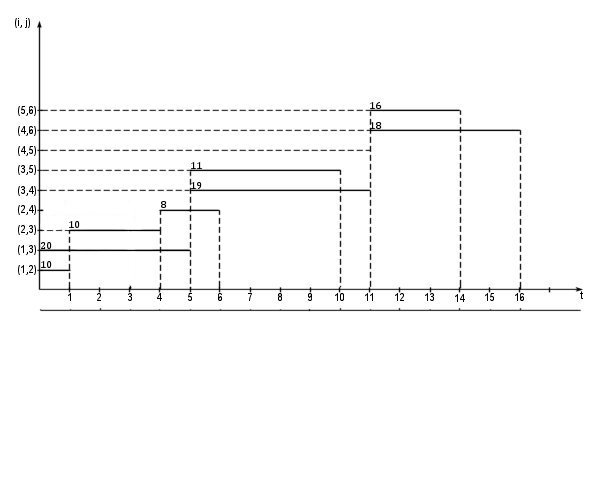





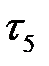
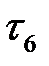
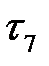
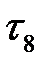
Рисунок 15.7
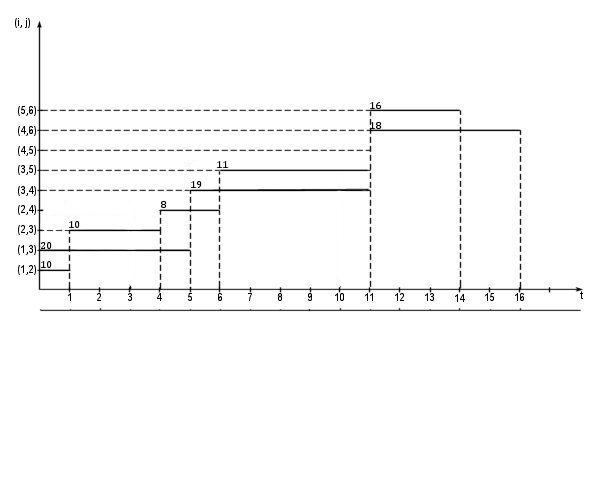






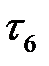
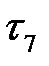
Рисунок 15.8
7. На промежутке  = (6, 11) интенсивность потребления
= (6, 11) интенсивность потребления  + +
+ +  =19+11=30 равна наличному запасу ресурса. Времена начала этих работ оставляем без изменения.
=19+11=30 равна наличному запасу ресурса. Времена начала этих работ оставляем без изменения.
8. На промежутке  интенсивность потребления
интенсивность потребления  = =18+16=34 > 30. Так как Rn(4, 6) = 0, Rn(5, 6) = 2, то следует сделать сдвиг работы (5, 6) до момента
= =18+16=34 > 30. Так как Rn(4, 6) = 0, Rn(5, 6) = 2, то следует сделать сдвиг работы (5, 6) до момента  = 16. Однако это приведет к удалению общей продолжительности реализации работ до величины 16+3=19.
= 16. Однако это приведет к удалению общей продолжительности реализации работ до величины 16+3=19.
Можно поступить иначе. Работа (5, 6) имеет резерв времени 2 дня. Увеличим ее продолжительность с 3 до 4 дней, сократив количество человек, занятых ежедневно на этом участке до 12 (3∙16 = 4∙12). В результате получим окончательный линейный график (рисунок 15.9, а) и эпюру ежедневной потребности в трудовых ресурсах (рисунок 15.9, б). Интенсивность использования трудовых ресурсов приведена в соответствие с ограничениями на ресурсы без изменения критического пути.
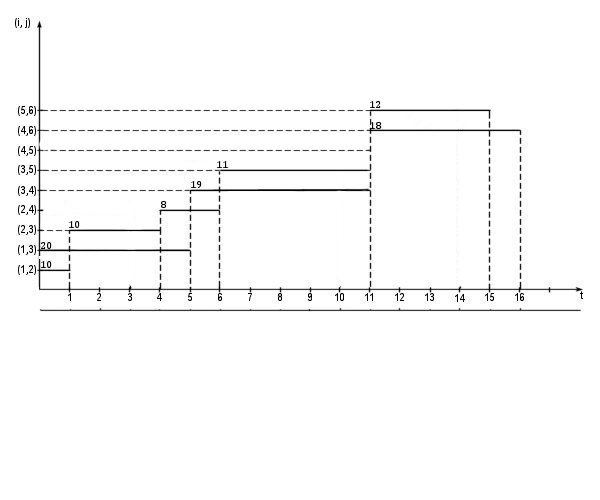








Рисунок 15.9, 
| Srij |
| t |
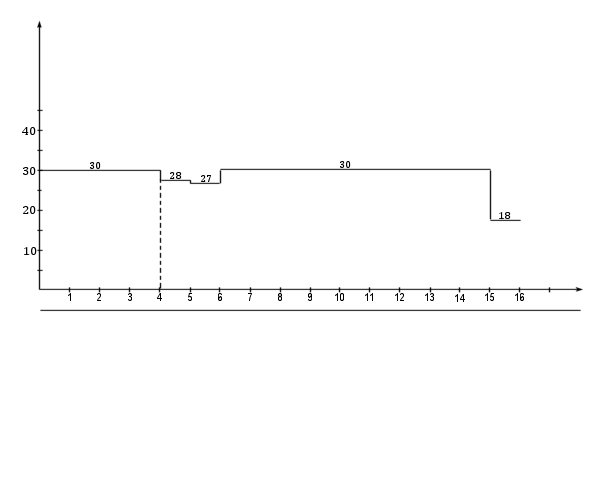








Рисунок 15.9,  . Эпюра ежедневной потребности в трудовых ресурсах.
. Эпюра ежедневной потребности в трудовых ресурсах.
Литература
1. Кузнецов А.В., Сакович В.А., Холод Н.И. – Высшая математика: Математическое программирование. – Мн.: Выш. шк., 1994.
2. Кузнецов А.В., Костевич Л.С., Холод Н.И. – Руководство к решению задач по математическому программированию. - Мн.: Выш. шк., 2001.
3. Холод Н.И. и др. Экономико – математические методы и модели. – Мн.: БГЭУ, 2000.
ОГЛАВЛЕНИЕ
Предисловие. 3
Введение. 4
Экономико-математическое моделирование как средство для принятия эффективных решений. 4
Лекция 1 Экономико-математические методы и модели оптимального планирования в промышленности, АПК.. 6
1.1.. Оптимальное планирование деятельности промышленных и сельскохозяйственных предприятий. Линейные оптимизационные модели. 6
1.1.. Примеры линейных оптимизационных моделей. 8
1.2.. Графический способ решения линейных оптимизационных моделей 14
1.3.. Свойства решений линейной оптимизационной модели. 20
Лекция 2 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение) 24
2.1.. Понятие о симплексном методе. 24
2.2.. Построение начального опорного плана. 25
2.3.. Признак оптимальности опорного плана. 28
Лекция 3 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение) 35
3.1.. Понятие двойственности. Построение двойственных моделей оптимального планирования в промышленности, АПК.. 35
3.2.. Соответствие между переменными пары взаимно двойственных линейных оптимизационных моделей. 37
3.3.. Теоремы двойственности. 46
Лекция 4 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение) 52
4.1.. Целочисленные оптимизационные модели в промышленности, АПК. Примеры. Методы решения. 52
4.2.. Алгоритм метода Гомори решения целочисленных оптимизационных моделей. 54
Лекция 5 Экономико-математические методы и модели оптимального планирования в промышленности, АПК (продолжение) 60
5.1.. Математическая модель транспортной задачи. 60
5.2.. Признак разрешимости транспортной модели. 62
5.3.. Построение начального опорного плана. 63
5.4.. Метод потенциалов построения оптимального опорного плана. 65
Лекция 6 Экономико-математические методы и модели финансов и кредита. 72
6.1.. Модели в сфере финансово-кредитной деятельности. Основные понятия. 72
6.2.. Модели матричных игр. 73
6.2.1 Модели матричных игр и их решение в чистых стратегиях. 73
6.2.2 Модели матричных игр со смешанными стратегиями игроков. Свойства смешанных стратегий. 78
6.2.3 Решение моделей матричных игр сведением к паре взаимно двойственных линейных оптимизационных моделей. 82
Лекция 7 Экономико-математические методы и модели финансов и кредита (продолжение) 91
7.1.. Статистические модели в сфере финансово-кредитной деятельности. 91
7.2.. Правила выбора оптимальной стратегии. 92
Лекция 8 Модель межотраслевого баланса в системе национальных счетов. 97
8.1.. Схема модели межотраслевого баланса в системе национальных счетов. 97
8.2.. Математическая модель отчетного межотраслевого баланса. 100
8.3.. Экономическая сущность и свойства коэффициентов прямых и полных затрат. 102
Лекция 9 Модель межотраслевого баланса в системе национальных счетов (продолжение) 105
9.1.. Использование модели МОБ в исследовании взаимосвязи отраслевых структур валового выпуска и конечного спроса. 105
9.2.. Использование статической модели МОБ в прогнозировании цен. 108
Лекция 10 Экономико-математические методы и модели управления социально-культурной сферой. 112
10.1 Применение экономико-математических моделей управление запасами в сфере услуг. Основные понятия теории управления запасами. 112
10.2 Однопродуктовые детерминированные модели со статическим спросом. 113
10.2.1 Простейшая модель оптимального размера партии поставки (модель Уилсона) 113
10.2.2 Свойства модели Уилсона. 116
10.2.3 Учет точки заказа. 117
10.2.4 Учет дискретности спроса  .. 120
.. 120
Лекция 11 Экономико-математические методы и модели управления социально-культурной сферой (продолжение) 123
11.1 Однопродуктовые детерминированные модели со статическим спросом (продолжение) 123
11.1.1 Модели с конечной интенсивностью поступления заказа. 123
11.1.2 Модель с дефицитом, когда неудовлетворенные требования ставятся на учет. 127
11.1.3 Обобщенная модель оптимальной партии поставки с постоянной интенсивностью и с учетом неудовлетворенных требований. 131
11.1.4 Модель в условиях скидки на размер заказа. 136
Лекция 12 Экономико-математические методы и модели управления социально-культурной сферой (продолжение) 141
12.1 Многопродуктовые модели управления производством, поставками и запасами. 141
12.1.1 Раздельная оптимизация. 141
12.1.2 Полное совмещение заказов. 148
12.2 Модели управления запасами со случайным спросом. 151
12.2.1 Однопериодная модель со случайным спросом. 151
12.2.2 Модель при наличии страхового запаса. 155
Лекция 13 Экономико-математические методы и модели во внешнеэкономической и в коммерческой деятельности. 161
13.1 Экономико-математические методы сетевого планирования и управления во внешнеэкономической и в коммерческой деятельности. 161
13.2 Виды сетевых моделей и правила их построения. 164
13.3 Определение продолжительности работ. 168
Лекция 14 Экономико-математические методы и модели во внешнеэкономической и в коммерческой деятельности (продолжение) 170
14.1 Расчет параметров сетевого графика. 170
14.1.1 Виды путей сетевого графика. Критический путь и алгоритм его нахождения. 170
14.1.2 Ранние и поздние сроки свершения событий. Резерв времени событий. 171
14.1.3 Ранние и поздние сроки начала и окончания работ. Определение резервов времени работ. Полный резерв времени работ. 174
Лекция 15 Экономико-математические методы и модели во внешнеэкономической и в коммерческой деятельности (продолжение) 178
15.1 Оптимизация сетевых графиков. 178
15.1.1 Оптимизация проекта по времени. 178
15.1.2 Оптимизация проекта по ресурсам. 184
Литература. 191
Учебное издание
Булдык Георгий Митрофанович
Доктор педагогических наук
Профессор
Дата добавления: 2015-09-29; просмотров: 2533;
