Виды путей сетевого графика. Критический путь и алгоритм его нахождения

Любая последовательность работ сетевого графика, в которой конечное событие каждой работы совпадает с начальным событием следующей за ней работы, называется путем.

Путь сетевого графика, в котором начальная точка совпадает с исходным событием, а конечная – с завершающим событием, называется полным.

Путь от исходного события до любого взятого предшествует данному событию. Предшествующий событию путь, имеющий наибольшую длину, называется максимальным предшествующим. Он обозначается L₁(i), а его продолжительность t[L₁(i)].

Путь, соединяющий любое взятое событие с завершающим, называется последующим путем. Такой путь с наибольшей длиной называется максимально последующим и обозначается L₂(i), а его продолжительность t[L₂(i)].

Полный путь, имеющий наибольшую длину, называется критическим. Пути, отличные от критического, называются ненапряженными. Они имеют резервы времени.

Работы критического пути выделяются жирными линиями или двойными. Продолжительность критического пути считается главным параметром графика.

Рассмотрим алгоритм определения критического пути на сетевом графике, использующий алгоритм метода динамического программирования.

Упорядочим вершины графика по рангам и пронумеруем их с конца к началу. Это позволит совместить номера рангов с этапами попятного движения при отыскании условно-оптимальных управлений на последнем, двух последних и т.д. этапах. Нахождение критического пути разберем на примере сетевого графика, изображенного на рисунке 14.1.

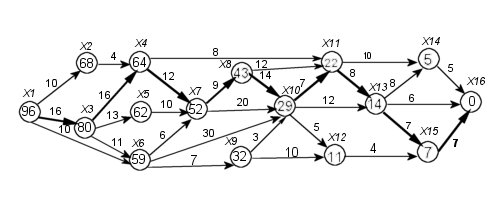
Рисунок 14.1

Согласно принципу оптимальности Беллмана, оптимальное управление на каждом этапе определяется целью управления и состоянием на начало этапа. Состояние системы – это события, лежащие на рангах. Для совершения конечного события Х₁₆ необходимо совершение предшествующих событий. Возможные состояния системы на начало последнего этапа работ – совершение событий Х₁₄ и Х_15. В кружках у точек Х₁₄ и Х₁₅ поставим максимальную продолжительность работ на последнем этапе: Х₁₄ 5 , Х₁₅ 7 . Найдем максимальную продолжительность работ на двух последних этапах. Состояние системы на начало предпоследнего этапа обусловлено событием Х_13. Максимальная продолжительность пути, ведущая из Х₁₃ к Х₁₆ равна . Следовательно, в кружке у события Х₁₃ нужно поставить число 14 и т.д. Проводя этапы от конца к началу, узнаем длину критического пути t_кр=96. Чтобы найти сам критический путь, процесс вычислений пройдем от начального события Х₁ к конечному Х₁₆. Число 96 на первом этапе (от начала) мы получили, прибавив 16 к числу 80. Следовательно, критический путь на этом этапе будет равен (Х₁, Х₃). Число 80=16+64. Следовательно, критический путь на втором этапе проходит через работу (Х₃, Х₄) и т.д. На графике он выделен жирной линией:

X₁ – X₃ – X₄ – X₇ – X₈ – X₁₀ – X₁₁ – X₁₂ – X₁₃ – X₁₅ – X₁₆ .