Проекция вектора на ось. Как и на плоскости (см. § 8.1), векторы в пространстве определяются как направленные отрезки, для которых вводятся операции сложения (правило треугольника

Как и на плоскости (см. § 8.1), векторы в пространстве определяются как направленные отрезки, для которых вводятся операции сложения (правило треугольника, параллелограмма для двух векторов и правило ломаной для n векторов) и умножения на число. Эти операции обладают теми же свойствами, что и операции на плоскости.

Векторы называются компланарными, если они лежат в параллельных плоскостях (или в одной плоскости). Для трех некомпланарных векторов 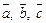справедливо сложение по правилу параллелепипеда:

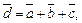
где 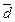– диагональ параллелепипеда, построенного на векторах 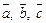с общим началом, с тем же началом (рис. 14.1).

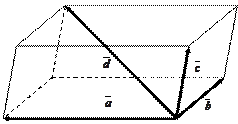
Рис. 14.1

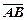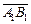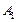Геометрической проекцией вектора на ось l называется вектор , где и 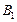– основания перпендикуляров, опущенных на ось из точек A и B соответственно (рис. 14.2).

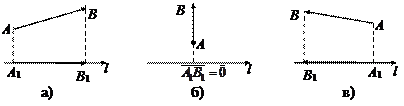
Рис. 14.2

Если 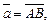то 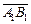является геометрической проекцией (или составляющей) вектора 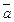на ось l и обозначается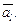

Алгебраической проекцией (просто проекцией) вектора 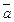на ось l называется число 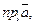которое определяется следующим образом:

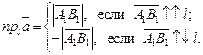
Запись 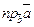обозначает проекцию вектора 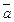на направление вектора 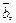т. е. на ось, определяемую ортом