Над векторами в координатной форме
Векторы 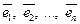 называются линейно-независимыми, если равенство
называются линейно-независимыми, если равенство 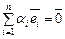 справедливо тогда и только тогда, когда
справедливо тогда и только тогда, когда 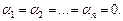 В противном случае эти векторы называются линейно-зависимыми. Для того чтобы векторы
В противном случае эти векторы называются линейно-зависимыми. Для того чтобы векторы 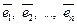 были линейно-зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
были линейно-зависимыми, необходимо и достаточно, чтобы хотя бы один из них можно было представить в виде линейной комбинации остальных.
Упорядоченная тройка 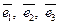 ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Это значит, что любой вектор
ненулевых линейно-независимых векторов образует базис в трехмерном пространстве. Это значит, что любой вектор 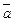 этого пространства единственным образом может быть представлен в виде
этого пространства единственным образом может быть представлен в виде
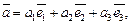
где 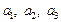 – координаты вектора
– координаты вектора 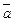 в базисе
в базисе 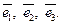 Записывают:
Записывают: 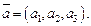
В физическом пространстве линейная независимость векторов равносильна их некомпланарности. Таким образом, любая тройка ненулевых некомпланарных векторов, взятых в определенном порядке, образует базис этого пространства.
Пусть задана тройка 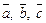 некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора
некомпланарных векторов. Совместим начала этих векторов. Если кратчайший поворот вектора 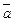 до направления вектора
до направления вектора 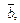 наблюдаемый с конца вектора
наблюдаемый с конца вектора 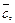 совершается против часовой стрелки, то тройка векторов
совершается против часовой стрелки, то тройка векторов 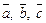 называется правой. В противном случае – левой. Всюду далее будем рассматривать правые тройки базисных векторов.
называется правой. В противном случае – левой. Всюду далее будем рассматривать правые тройки базисных векторов.
Совокупность базисных векторов и их общего начала образует, говорят, аффинную систему координат в пространстве. Координаты векторов в таком случае называют аффинными.
Если даны два вектора 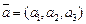 и
и 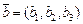 в некотором базисе, то
в некотором базисе, то 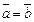 тогда и только тогда, когда
тогда и только тогда, когда 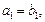
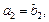
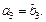
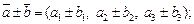 (14.2)
(14.2)
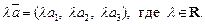 (14.3)
(14.3)
В случае, когда базисные векторы попарно перпендикулярны, система координат называется прямоугольной декартовой системой координат. Если добавить, кроме того, условие нормированности базисных векторов (или их единичную длину), то получим ортонормированный базис, который обозначают 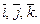 Таким образом,
Таким образом, 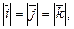
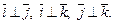 Прямоугольные декартовы координаты вектора
Прямоугольные декартовы координаты вектора 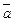 является его проекциями на векторы
является его проекциями на векторы 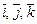 соответственно. В частности, если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом
соответственно. В частности, если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом 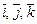 , то радиус-вектор
, то радиус-вектор 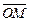 равен
равен
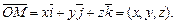
Если 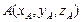 и
и 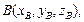 то
то
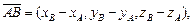
а длина 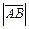 этого вектора может быть найдена по формуле
этого вектора может быть найдена по формуле
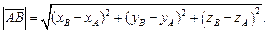
Линейные операции для векторов 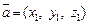 и
и 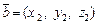 в координатной форме и их скалярное произведение вычисляются по формулам:
в координатной форме и их скалярное произведение вычисляются по формулам:
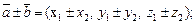 (14.4)
(14.4)
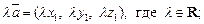 (14.5)
(14.5)
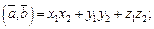 (14.6)
(14.6)
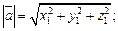 (14.7)
(14.7)
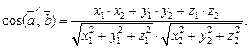 (14.8)
(14.8)
Направляющими косинусами вектора 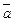 называются величины
называются величины 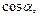
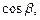
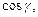 где
где 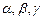 – углы, которые образует вектор
– углы, которые образует вектор 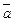 соответственно с осями Ox, Oy, Oz. Их вычисляют по формулам:
соответственно с осями Ox, Oy, Oz. Их вычисляют по формулам:
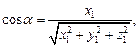
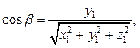 (14.9)
(14.9)
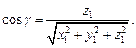
Если 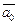 – единичный вектор, то
– единичный вектор, то 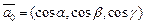 .
.
Координаты точки C, делящей отрезок AB в отношении 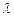
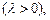 можно найти по формулам:
можно найти по формулам:
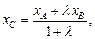
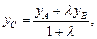
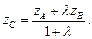 (14.10)
(14.10)
Пример 1. Даны векторы 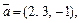
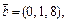
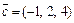 в некотором базисе. Найти координаты вектора
в некотором базисе. Найти координаты вектора 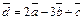 в этом базисе.
в этом базисе.
Решение.Определим координаты вектора 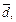 следуя правилам действий над векторами в координатной форме, т. е.
следуя правилам действий над векторами в координатной форме, т. е.
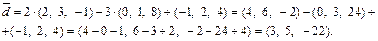
В дальнейшем, если не оговорено противное, все координаты считаются заданными в ортонормированном базисе.
Пример 2. Вычислить проекцию вектора 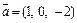 на направление вектора
на направление вектора 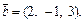
Дата добавления: 2015-09-29; просмотров: 904;
