Решение. Пример 3. Найти направляющие косинусы вектора
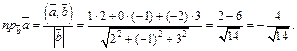
Пример 3. Найти направляющие косинусы вектора 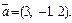
Решение. Используем формулы (14.9):
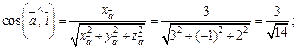
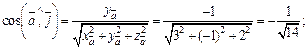
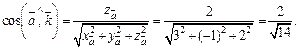
Пример 4. Найти прямоугольные декартовы координаты вектора 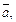 если
если 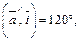
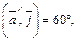
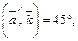
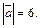
Решение.Пусть 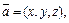 тогда
тогда
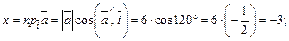
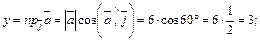
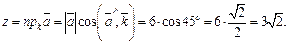
Итак, 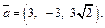
Пример 5. Даны векторы 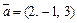 и
и 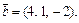 Вычислить:
Вычислить:
1) 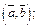 2)
2) 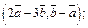 3)
3) 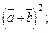 4)
4) 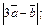
5) 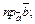 6)
6) 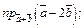 7)
7) 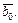
Решение. 1) Используем формулу (14.6):
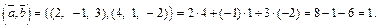
2) Сначала вычислим координаты векторов 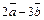 и
и 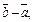 используя формулы (14.4) и (14.5):
используя формулы (14.4) и (14.5):
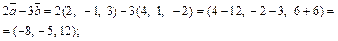
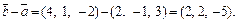
Тогда согласно формуле (14.6) получим:
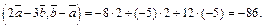
3) Найдем координаты суммы векторов:
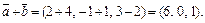
Далее, используя формулу скалярного квадрата и формулу (14.7) длины вектора, получим:
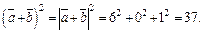
4) Вычислим координаты вектора 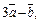 используя формулы (14.4) и (14.5):
используя формулы (14.4) и (14.5):
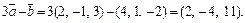
Тогда по формуле (14.7) получим:
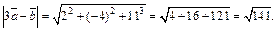
5) По формуле (14.1) получим:
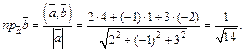
6) Используя формулы (14.1), (14.4)–(14.7), получим:
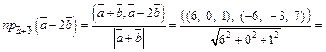
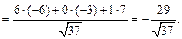
7) Вектор 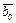 – это единичный вектор направления вектора
– это единичный вектор направления вектора 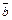 :
:
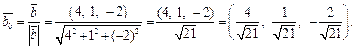
Пример 6. Вектор 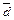 перпендикулярен векторам
перпендикулярен векторам  и
и 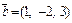 и удовлетворяет условию
и удовлетворяет условию 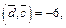 где
где 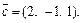 Найти координаты вектора
Найти координаты вектора 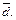
Решение. Пусть 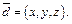 По условию
По условию 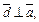 что влечет
что влечет 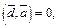 т. е.
т. е.  Аналогично из условия
Аналогично из условия 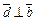 получаем
получаем 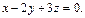 Наконец, из
Наконец, из 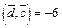 имеем
имеем 
Получили систему уравнений
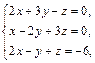
Решая которую, придем к ответу:
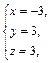 т. е.
т. е. 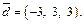
Пример 7. Даны векторы 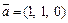 и
и 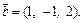 Найти косинус угла между векторами
Найти косинус угла между векторами 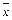 и
и 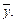 для которых
для которых 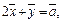
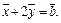
Решение. Выразим векторы 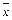 и
и 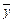 через
через 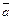 и
и 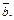 Из равенства
Из равенства 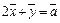 получим
получим 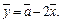 Тогда, используя
Тогда, используя 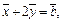 получим:
получим:
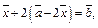 т. е.
т. е. 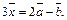
Далее находим координаты вектора 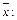
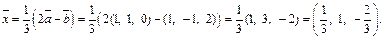
Поскольку 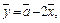 то
то
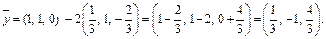
Используя формулу (14.8), находим:
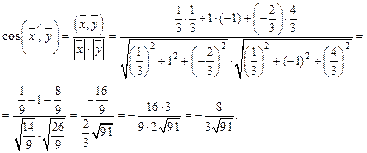
Пример 8. Луч образует с векторами 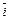 и
и 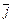 углы соответственно
углы соответственно 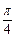 и
и 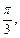 а с вектором
а с вектором 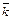 – тупой угол. Найти этот угол.
– тупой угол. Найти этот угол.
Решение. Рассмотрим единичный вектор 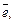 сонаправленный с заданным лучом. Он определяется направляющими косинусами, т. е.
сонаправленный с заданным лучом. Он определяется направляющими косинусами, т. е. 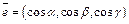 . Так как
. Так как 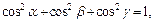 то имеем
то имеем 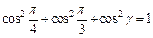 или
или 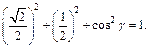 Из последнего равенства имеем
Из последнего равенства имеем 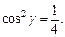 По условию γ – тупой угол. Значит,
По условию γ – тупой угол. Значит, 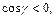 т. е.
т. е. 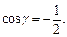
Таким образом, искомый угол равен 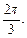
Пример 9. Показать, что векторы 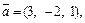
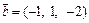 и
и 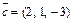 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 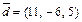 в этом базисе.
в этом базисе.
Решение.1-й способ. В трехмерном пространстве базис образуют любые три линейно-независимых вектора с ненулевой длиной. Определим, будут ли три заданные вектора линейно-независимыми. Для этого составим их линейную комбинацию с коэффициентами 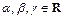 и приравняем к
и приравняем к 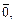 т. е. рассмотрим:
т. е. рассмотрим:
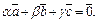
Если окажется, что при этом 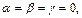 то система этих векторов линейно-независима, а значит, они образуют базис.
то система этих векторов линейно-независима, а значит, они образуют базис.
Векторному равенству 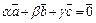 в координатной форме соответствует следующее условие:
в координатной форме соответствует следующее условие:
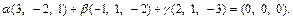
Из определения равенства двух векторов имеем систему
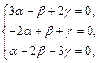
решая которую, получим 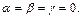
Найдем в этом базисе координаты вектора 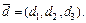
Так как 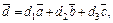 то в координатной форме
то в координатной форме
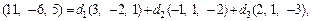
что приводит к системе линейных уравнений
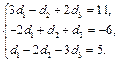
Решая последнюю систему каким-либо методом, получим 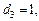
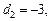
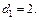 Это значит что в базисе
Это значит что в базисе 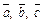 вектор
вектор 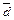 имеет координаты:
имеет координаты: 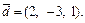
2-й способ. Векторы образуют базис пространства, если они некомпланарны. Это равносильно тому, что их смешанное произведение не равно 0, т. е. (в координатной форме)
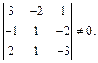
Вычисление последнего определителя показывает, что он не нулевой. Таким образом, векторы 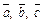 образуют базис. Найти координаты вектора
образуют базис. Найти координаты вектора 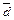 в этом базисе можно, как в 1-м способе.
в этом базисе можно, как в 1-м способе.
Пример 10. Векторы 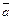 и
и 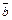 не коллинеарны. Найти, при каком a векторы
не коллинеарны. Найти, при каком a векторы 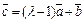 и
и 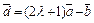 будут коллинеарны.
будут коллинеарны.
Решение. Если 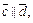 то существует такое число
то существует такое число 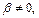 что
что 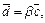 т. е.
т. е.
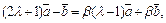 откуда
откуда
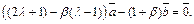
Векторы 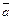 и
и 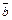 не коллинеарны, поэтому
не коллинеарны, поэтому
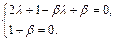
Решая эту систему, находим 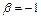 и
и 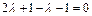 или
или 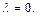 Таким образом, при
Таким образом, при 
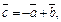
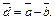 Как легко видеть, векторы
Как легко видеть, векторы 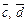 противоположны, т. е.
противоположны, т. е. 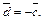
Дата добавления: 2015-09-29; просмотров: 1797;
