Свойства векторного произведения
1. 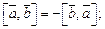
2. 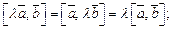
3. 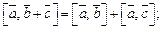
4. 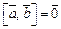 при
при 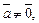
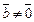 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 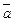 и
и 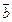 коллинеарны.
коллинеарны.
Если векторы 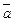 и
и 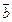 заданы в ортонормированном базисе и
заданы в ортонормированном базисе и 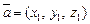 и
и 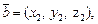 то
то
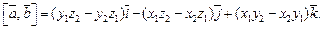
Последнюю формулу удобно записать в виде формального определителя третьего порядка
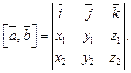
Пример 1. Пусть 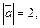
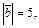
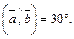 Найти:
Найти:
1) 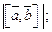 2)
2) 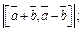 3)
3) 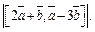
Решение.1) По определению векторного произведения векторов 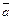 и
и 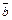 его длина
его длина
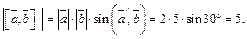
2) Используя алгебраические свойства векторного произведения, имеем:
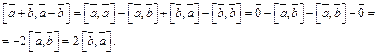
Значит, 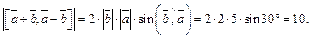
3) Используя свойства векторного произведения и условие задачи, получим:
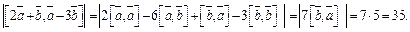
Пример 2. Упростить выражение:
1) 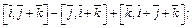
2) 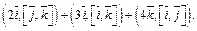
Решение.Воспользуемся равенствами 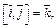
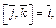
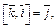
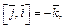
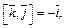
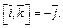
Тогда имеем:
1) 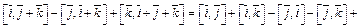
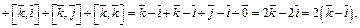
2) 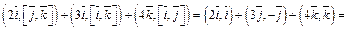
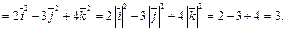
Пример 3. Вычислить площадь параллелограмма, диагоналями которого служат векторы 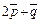 и
и 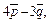 где
где 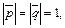
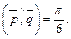
Решение. Используем известную из планиметрии формулу площади параллелограмма и геометрический смысл векторного произведения:
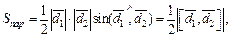
где 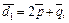
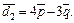
Тогда по свойствам векторного произведения получим:
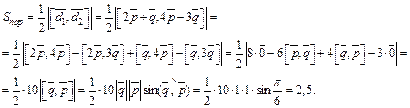
Пример 4. Вычислить площадь треугольника ABC и его высоту, опущенную из вершины A к стороне BC, если A(1, 1, 1), B(4, 2, –1), C(2, 3, 0).
Решение. Используем тот факт, что 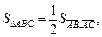 где
где 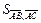 – площадь параллелограмма, построенного на векторах
– площадь параллелограмма, построенного на векторах 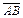 и
и 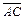 . Так как
. Так как 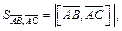 найдем сначала
найдем сначала 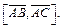
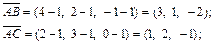
Вычисляем векторное произведение в координатной форме:
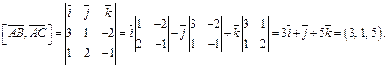
Тогда 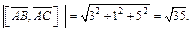
Значит, 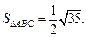
Для нахождения высоты h треугольника ABC воспользуемся формулой 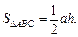 Тогда
Тогда 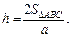 здесь
здесь 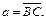
Значит
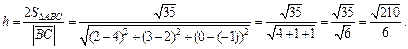
Пример 5. Даны три силы: 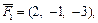
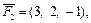
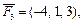 приложенные к точке A(–1, 4, 2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки O(2, 3, –1).
приложенные к точке A(–1, 4, 2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки O(2, 3, –1).
Решение. Пусть сила 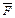 – равнодействующая сил
– равнодействующая сил 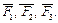 Тогда
Тогда 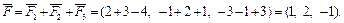 Значит момент
Значит момент 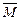 этой силы равен
этой силы равен
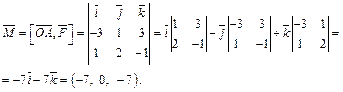
Вычисляем 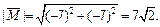 Для нахождения направляющих косинусов используем формулы (14.9):
Для нахождения направляющих косинусов используем формулы (14.9):
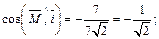
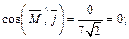
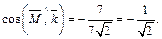
Дата добавления: 2015-09-29; просмотров: 959;
