Свойства смешанного произведения
1. 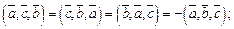
2. 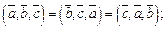
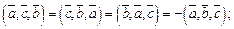
3. 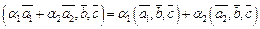 , где
, где 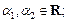
4. 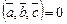 при
при 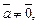
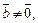
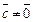 тогда и только тогда, когда
тогда и только тогда, когда 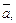
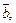
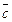 – компланарные векторы;
– компланарные векторы;
5. векторы 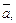
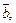
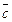 образуют базис в трехмерном пространстве при условии
образуют базис в трехмерном пространстве при условии 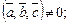
6. если 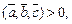 то векторы
то векторы 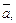
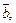
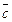 образуют правую тройку; если
образуют правую тройку; если 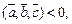 – левую.
– левую.
В случае, когда векторы 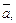
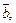
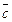 заданы в ортонормированном базисе координатами
заданы в ортонормированном базисе координатами 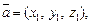
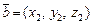 и
и 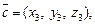 их смешанное произведение может быть найдено по формуле
их смешанное произведение может быть найдено по формуле
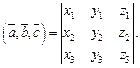 (14.11)
(14.11)
Пример 1. Векторы 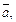
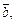
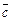 образуют правую тройку, взаимно перпендикулярны и
образуют правую тройку, взаимно перпендикулярны и 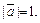
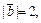
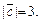 Вычислить их смешанное произведение.
Вычислить их смешанное произведение.
Решение. По определению 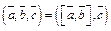 . Вектор
. Вектор 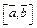 образует с
образует с 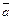 и
и 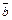 правую тройку, причем
правую тройку, причем 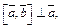
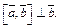 Значит,
Значит, 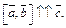 Кроме того,
Кроме того, 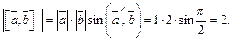 Тогда
Тогда 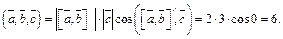
Пример 2. Для векторов 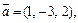
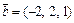 и
и 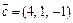 найти объем параллелепипеда, построенного на векторах
найти объем параллелепипеда, построенного на векторах 
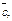 приведенных к общему началу, и определить ориентацию этой тройки векторов.
приведенных к общему началу, и определить ориентацию этой тройки векторов.
Решение.Используем формулу (4.11) для вычисления смешанного произведения в координатной форме:
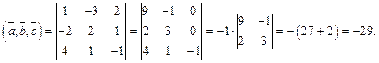
Поскольку получили отрицательное значение, то тройка векторов 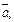
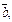
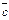 является левой, а объем параллелепипеда равен модулю смешанного произведения, т. е.
является левой, а объем параллелепипеда равен модулю смешанного произведения, т. е.
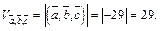
Пример 3. Доказать, что точки A(1, 2, –1), B(0, 1, 5), C(–1, 2, 1) и D(2, 1, 3) лежат в одной плоскости.
Решение. Рассмотрим три вектора:
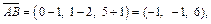
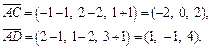
Вычисляем их смешанное произведение:
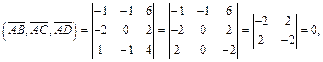
Поскольку оно равно нулю, то это значит, что векторы 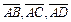 – компланарны. Они лежат в одной плоскости, так как имеют общее начало. Таким образом, точки A, B, C и D лежат в одной плоскости.
– компланарны. Они лежат в одной плоскости, так как имеют общее начало. Таким образом, точки A, B, C и D лежат в одной плоскости.
Пример 4. Вычислить объем тетраэдра OABC, если 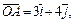
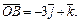
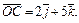
Решение. Используем формулу
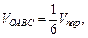
где 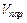 – объем параллелепипеда, построенного на векторах
– объем параллелепипеда, построенного на векторах 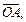
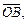
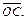 Объем параллелепипеда вычисляется через смешанное произведение
Объем параллелепипеда вычисляется через смешанное произведение
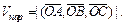
Поскольку
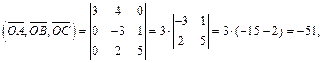
то 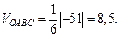
Пример 5. Вершины треугольника расположены в точках A(1, 1, 1), B(2, 3, 2) и C(4, 2, 5). Найти расстояние от точки D(5, 3, 6) до плоскости 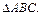
Решение. Убедимся, что точка D не лежит в одной плоскости с точками A, B и C, для чего найдем смешанное произведение векторов 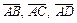 . Если оно будет не нулевым, то тем самым будет доказано, что векторы
. Если оно будет не нулевым, то тем самым будет доказано, что векторы 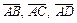 не являются компланарными, а значит, точки A, B, C, D не лежат в одной плоскости.
не являются компланарными, а значит, точки A, B, C, D не лежат в одной плоскости.
Так как 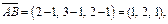
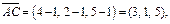
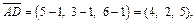 то смешанное произведение равно
то смешанное произведение равно
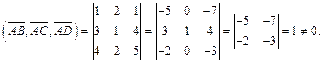
Значит, 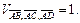
Поскольку расстояние h от точки D до плоскости 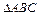 численно равно высоте параллелепипеда, опущенной из вершины D на основание, в котором лежит
численно равно высоте параллелепипеда, опущенной из вершины D на основание, в котором лежит 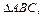 то из формулы
то из формулы 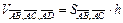 находим
находим
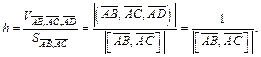
Найдем 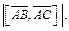 Поскольку
Поскольку
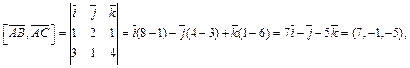
то 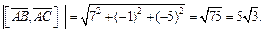
Таким образом, 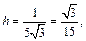 т. е. искомое расстояние равно
т. е. искомое расстояние равно 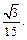
Пример 6. Доказать, что векторы 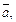
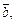
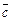 компланарны, если
компланарны, если 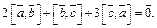 .
.
Решение. Умножим скалярно данное равенство на вектор 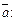
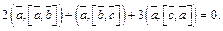
Так как 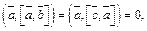 то
то 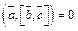 или векторы
или векторы 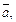
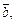
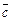 компланарны.
компланарны.
Доказанное можно обобщить на случай, когда задано равенство 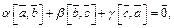 где
где 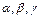 – числа, среди которых, по крайней мере, есть одно ненулевое.
– числа, среди которых, по крайней мере, есть одно ненулевое.
Дата добавления: 2015-09-29; просмотров: 4217;
