Расположение прямых
Пусть L – прямая, для которой необходимо составить уравнения, 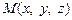 – произвольная точка этой прямой.
– произвольная точка этой прямой.
1. Если известны координаты направляющего вектора 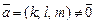 прямой L и некоторой фиксированной ее точки
прямой L и некоторой фиксированной ее точки 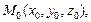 то уравнение
то уравнение
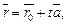 (15.12)
(15.12)
где 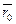 – радиус-вектор точки
– радиус-вектор точки 
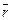 – радиус-вектор произвольной точки,
– радиус-вектор произвольной точки,  называется векторно-параметрическим уравнением прямой L. В координатной форме уравнение (15.12) равносильно трем параметрическим уравнениям:
называется векторно-параметрическим уравнением прямой L. В координатной форме уравнение (15.12) равносильно трем параметрическим уравнениям:
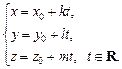 (15.13)
(15.13)
Система (15.13) определяет параметрические уравнения прямой L.
По исходной информации получаем также канонические уравнения прямой L:
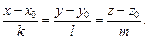 (15.14)
(15.14)
2. Пусть известны две точки 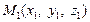 и
и 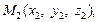 лежащие на прямой L. Тогда векторы
лежащие на прямой L. Тогда векторы 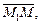
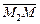 коллинеарны, и можно записать уравнения прямой, проходящей через две точки:
коллинеарны, и можно записать уравнения прямой, проходящей через две точки:
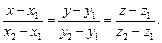 (15.15)
(15.15)
3. В пространстве прямую можно задать как линию пересечения двух плоскостей:
 (15.16)
(15.16)
В уравнениях плоскостей (15.16) коэффициенты при переменных не являются пропорциональными (иначе плоскости либо параллельны, либо совпадают).
О взаимном расположении двух прямых в пространстве можно судить по их направляющим векторам.
Угол между прямыми можно определить через косинус угла между направляющими векторами.
Прямые параллельныпри условии коллинеарности их направляющих векторов (координаты пропорциональны).
Угол между прямыми прямой при условии перпендикулярности их направляющих векторов (скалярное произведение равно 0).
Прямые лежат в одной плоскости при условии компланарности их направляющих векторов и вектора 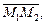 где М1 и М2 – точки этих прямых (смешанное произведение равно 0).
где М1 и М2 – точки этих прямых (смешанное произведение равно 0).
Расстояние от точки М0 до прямой L вычисляется по формуле
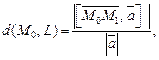 (15.17)
(15.17)
где 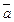 – направляющий вектор; М1 – точка прямой.
– направляющий вектор; М1 – точка прямой.
Эту формулу можно использовать и для нахождения расстояния между параллельными прямыми.
Если прямые L1 и L2 являются скрещивающимися, то расстояние между ними определяют по формуле
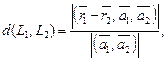 (15.18)
(15.18)
где 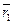 и
и 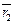 – радиус-векторы точек
– радиус-векторы точек  и
и 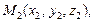 принадлежащих прямым L1 и L2 соответственно, а векторы
принадлежащих прямым L1 и L2 соответственно, а векторы 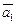 и
и 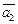 – направляющие векторы этих прямых.
– направляющие векторы этих прямых.
Пример 1. Составить канонические уравнения прямой, проходящей через:
1) точку 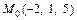 параллельно вектору
параллельно вектору 
2) две заданные точки 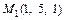 и
и 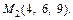
Решение. 1) Пусть 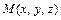 – произвольная точка искомой прямой. Тогда
– произвольная точка искомой прямой. Тогда 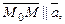 т. е. их координаты пропорциональны.
т. е. их координаты пропорциональны. 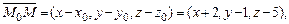
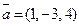 . Согласно (15.14) получаем уравнения
. Согласно (15.14) получаем уравнения
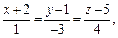
которые и представляют собой канонические уравнения прямой.
2) Пусть 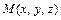 – произвольная точка прямой. Тогда, используя уравнение (15.15) для нашего случая, имеем:
– произвольная точка прямой. Тогда, используя уравнение (15.15) для нашего случая, имеем:
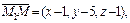
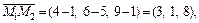 откуда
откуда
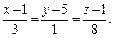
Это и есть искомый результат.
Пример 2. Записать канонические уравнения прямой, заданной системой уравнений двух плоскостей
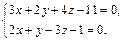
Решение. Для перехода к каноническим уравнениям прямой обычно поступают следующим образом. Подбирают какую-либо точку 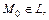 фиксируя числовое значение одной из координат и решая систему двух линейных уравнений с двумя неизвестными. Затем находят направляющий вектор
фиксируя числовое значение одной из координат и решая систему двух линейных уравнений с двумя неизвестными. Затем находят направляющий вектор 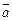 прямой L как векторное произведение нормальных векторов плоскостей, задающих прямую L. Реализуем этот подход на данном примере.
прямой L как векторное произведение нормальных векторов плоскостей, задающих прямую L. Реализуем этот подход на данном примере.
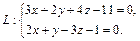
Имеем 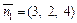 – нормальный вектор плоскости
– нормальный вектор плоскости 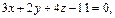
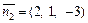 – нормальный вектор плоскости
– нормальный вектор плоскости 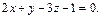
Тогда вектор 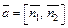 является направляющим вектором прямой L. Определим его координаты:
является направляющим вектором прямой L. Определим его координаты:
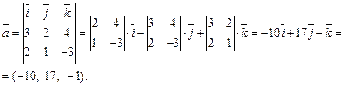
Для нахождения точки  зафиксируем одно из координатных значений, например,
зафиксируем одно из координатных значений, например, 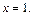 Тогда, подставив в заданные общие уравнения значение
Тогда, подставив в заданные общие уравнения значение 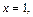 имеем:
имеем:
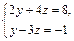 или
или 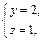 т. е.
т. е. 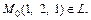
Таким образом, получаем искомые канонические уравнения заданной прямой L:
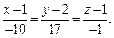
З а м е ч а н и е. Для нахождения точки 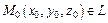 можно сначала решить систему в общем виде, а потом выбрать частное решение, а в качестве
можно сначала решить систему в общем виде, а потом выбрать частное решение, а в качестве 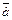 взять
взять 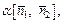 где
где 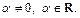
Пример 3. Доказать, что прямые L1 и L2 параллельны, и найти расстояние между ними, если они заданы параметрическими уравнениями:
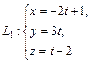 и
и 
Решение. Прямая L1 имеет направляющий вектор 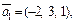 а L2 – вектор
а L2 – вектор  причем
причем  так как
так как  Значит,
Значит, 
Найдем расстояние 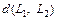 между ними, используя формулу расстояния (15.17) от точки до прямой. В параметрических уравнениях заданных прямых полагаем
между ними, используя формулу расстояния (15.17) от точки до прямой. В параметрических уравнениях заданных прямых полагаем 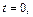 имеем
имеем 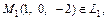
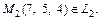 Тогда
Тогда 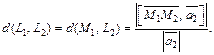
Вычисляем векторное произведение:

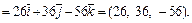
После этого находим длины нужных векторов:
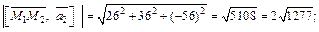
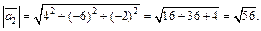
Значит, 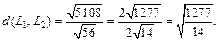
Пример 4. Доказать, что прямые L1 и L2 пересекаются, и найти координаты точки пересечения, если они заданы параметрическими уравнениями:
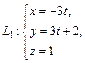 и
и 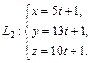
Решение. Координаты направляющего вектора прямой равны соответственно числовым коэффициентам при t, т. е. 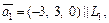
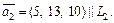 При этом
При этом 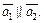 Значит
Значит 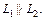
Прежде всего определим, лежат ли прямые в одной плоскости, т. е. являются ли векторы 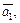
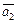 и
и 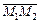 компланарными (здесь
компланарными (здесь 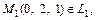
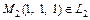 ). Найдем для этого их смешанное произведение:
). Найдем для этого их смешанное произведение:
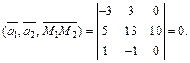
Значит, прямые лежат в одной плоскости и не параллельны. Следовательно, они пересекаются.
Найдем точку их пересечения 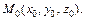
Поскольку  то
то 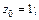
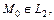 то
то 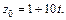
Получаем, что при подстановке 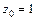 в уравнение прямой
в уравнение прямой 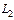
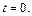
Значит, 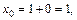
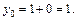 Итак,
Итак,  – точка пересечения заданных прямых.
– точка пересечения заданных прямых.
Пример 5. Доказать, что прямые L1 и L2 скрещиваются, найти расстояние между ними, если они заданы параметрическими уравнениями:
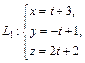 и
и 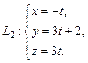
Решение. Направляющий вектор прямой L1 есть 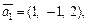 а прямой L2 – вектор
а прямой L2 – вектор 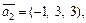 причем
причем 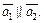 Значит
Значит 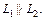 Определим, пересекаются ли прямые. Так как
Определим, пересекаются ли прямые. Так как 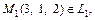
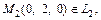 то условием пересечения прямых служит компланарность векторов
то условием пересечения прямых служит компланарность векторов 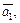
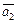 и
и 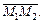 Найдем смешанное произведение этих векторов:
Найдем смешанное произведение этих векторов:
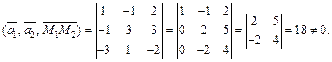 (15.19)
(15.19)
Значит, указанные векторы, а вместе с ними и прямые L1 и L2, не лежат в одной плоскости.
Прямые L1 и L2 скрещиваются, так как они не пересекаются и не параллельны. Найдем расстояние между ними по формуле (15.18), используя (15.19):
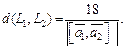
Определяем координаты:
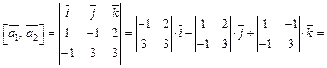
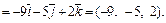
Тогда
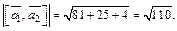
Получаем: 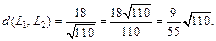
Дата добавления: 2015-09-29; просмотров: 1318;
