Предел функции в точке и на бесконечности
Определение предела функции по Гейне было дано в § 10.3.
Определение по Коши. Число А называется пределом функции f(x) в точке х0, если функция определена в некоторой выколотой окрестности точки х0 и если для любого сколь угодно малого числа 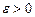 существует такое число
существует такое число 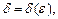 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
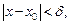 (16.1)
(16.1)
выполняется
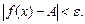 (16.2)
(16.2)
Это записывают так:
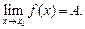
Число А называется пределом функции на бесконечности (при 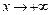 или
или 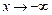 ), если для любого
), если для любого 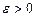 существует число
существует число 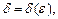 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
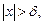
выполняется неравенство
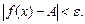
Это записывают так:
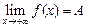 или
или 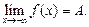
Определение предела функции в точке (на бесконечности) по Гейне и Коши эквивалентны.
Функция f(x) называется бесконечно большой при 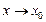
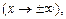 если для всякого числа М > 0 существует число
если для всякого числа М > 0 существует число 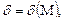 что для всех х, удовлетворяющих условию
что для всех х, удовлетворяющих условию
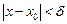 (
( 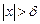 ),
),
выполняется неравенство
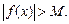
Это записывают так:
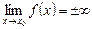
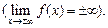
Если f(x) – бесконечно большая функция при 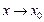
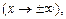 то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
то она не имеет предела в этой точке (на бесконечности). Символ предела в данном случае используют лишь для обозначения.
Функция f(x) называется бесконечно малой при 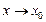
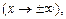 если
если
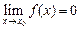
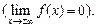
Дата добавления: 2015-09-29; просмотров: 1435;
