Прямая и плоскость в пространстве
Пусть прямая L задана каноническими уравнениями:
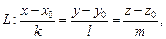
где 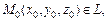
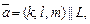 а плоскость P задана общим уравнением:
а плоскость P задана общим уравнением:
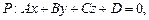
где 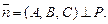
Тогда взаимное расположение прямой L и плоскости P в пространстве можно определить по взаимному расположению направляющего вектора 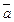 прямой L и нормального вектора
прямой L и нормального вектора 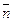 плоскости P. Справедливы утверждения:
плоскости P. Справедливы утверждения:
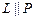 тогда и только тогда, когда
тогда и только тогда, когда 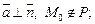
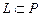 тогда и только тогда, когда
тогда и только тогда, когда 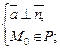
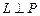 тогда и только тогда, когда
тогда и только тогда, когда 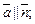
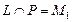 тогда и только тогда, когда
тогда и только тогда, когда 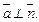
В последнем случае координаты точки пересечения М1 могут быть найдены следующим образом. От канонических уравнений прямой следует перейти к параметрическим, после чего подставить x = x(t), y = y(t), z = z(t) в уравнение плоскости. Затем надо разрешить полученное уравнение относительно параметра t и найденное значение t подставить в параметрические уравнения прямой. Это позволит найти значения x1, y1, z1, которые и будут координатами искомой точки М1 пересечения прямой L и плоскости P.
Углом j между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на плоскость, т. е.
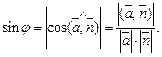
Пример 1. Установить взаимное расположение прямой и плоскости. В случае их пересечения найти координаты точки пересечения:
1) 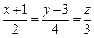 и
и 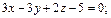
2) 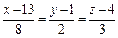 и
и 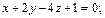
3) 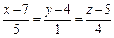 и
и 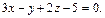
Решение. 1) Определим координаты направляющего вектора прямой 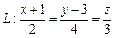 по ее каноническим уравнениям. Это вектор
по ее каноническим уравнениям. Это вектор 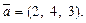 Нормальный вектор
Нормальный вектор 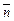 плоскости
плоскости 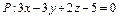 имеет координаты
имеет координаты 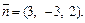 Найдем скалярное произведение векторов
Найдем скалярное произведение векторов 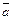 и
и 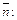
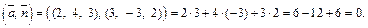
Значит, 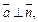 т. е. прямая L и плоскость P параллельны. Проверим, не лежит ли прямая L в плоскости P. Для этого определим, принадлежит ли плоскости P точка
т. е. прямая L и плоскость P параллельны. Проверим, не лежит ли прямая L в плоскости P. Для этого определим, принадлежит ли плоскости P точка 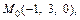 которая лежит на прямой. Подставим ее координаты в уравнение плоскости:
которая лежит на прямой. Подставим ее координаты в уравнение плоскости:
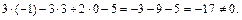
Следовательно, 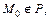 а значит,
а значит, 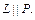
2) Прямая 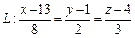 имеет направляющий вектор
имеет направляющий вектор 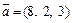 и проходит через точку
и проходит через точку 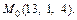 Выясним, будет ли вектор
Выясним, будет ли вектор 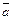 перпендикулярен нормальному вектору
перпендикулярен нормальному вектору 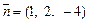 заданной плоскости
заданной плоскости 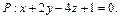 Вычислим скалярное произведение:
Вычислим скалярное произведение:
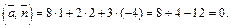
Поскольку оно равно нулю, то 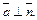
Осталось проверить принадлежность точки 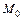 плоскости:
плоскости:
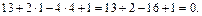
Значит, прямая L лежит в плоскости P.
3) Направляющий вектор 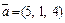 заданной прямой и нормальный вектор
заданной прямой и нормальный вектор 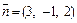 плоскости не коллинеарны и не перпендикулярны, так как
плоскости не коллинеарны и не перпендикулярны, так как 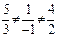 (коэффициенты не пропорциональны) и
(коэффициенты не пропорциональны) и 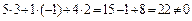 (скалярное произведение не равно нулю). Значит,
(скалярное произведение не равно нулю). Значит, 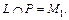 Найдем координаты точки М1 пересечения прямой и плоскости. Для этого перейдем сначала к параметрическим уравнениям прямой:
Найдем координаты точки М1 пересечения прямой и плоскости. Для этого перейдем сначала к параметрическим уравнениям прямой:
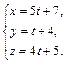
Затем в уравнение плоскости P подставим вместо x, y, z их выражение через параметр t:
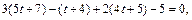
откуда имеем:
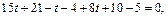 т. е.
т. е. 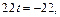
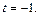
Подставим найденное значение параметра t в параметрические уравнения прямой: 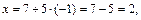
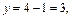
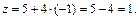
Получили точку 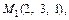 в которой прямая пересекает плоскость.
в которой прямая пересекает плоскость.
Пример 2. Определить угол между прямой L и плоскостью P:
1) 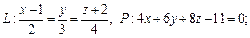
2) 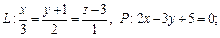
3) 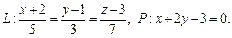
Решение. 1) По уравнению прямой L находим ее направляющий вектор 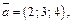 а для плоскости Р – нормальный вектор
а для плоскости Р – нормальный вектор 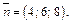
Очевидно, что координаты этих векторов пропорциональны, а значит, векторы являются коллинеарными. Следовательно, прямая L перпендикулярна плоскости Р, т. е. 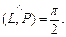
2) Направляющий вектор 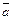 прямой L имеет координаты
прямой L имеет координаты 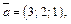 а нормальный вектор
а нормальный вектор 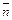 плоскости Р –
плоскости Р – 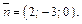 Так как
Так как 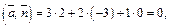 то векторы перпендикулярны, а прямая и плоскость параллельны. Определим, не лежит ли прямая L в плоскости. Для этого координаты точки
то векторы перпендикулярны, а прямая и плоскость параллельны. Определим, не лежит ли прямая L в плоскости. Для этого координаты точки 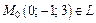 подставим в уравнение плоскости:
подставим в уравнение плоскости: 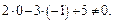 Значит прямая и плоскость параллельны, т. е.
Значит прямая и плоскость параллельны, т. е. 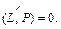
3) 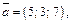
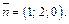 Значит,
Значит,
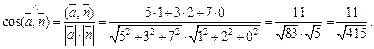
Таким образом 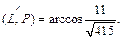
Пример 3. Найти координаты точки N, симметричной точке 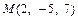 относительно прямой, проходящей через точки
относительно прямой, проходящей через точки 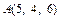 и
и 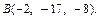
Решение. 1-й способ. Построим плоскость Р, проходящую через точку М перпендикулярно прямой АВ.
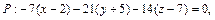
откуда Р: 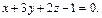
Уравнения прямой АВ: 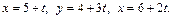
Найдем точку О пересечения плоскости Р и прямой АВ. Для этого решим уравнение
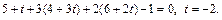 Значит, О(3, –2, 2). Так как О – середина отрезка MN, то
Значит, О(3, –2, 2). Так как О – середина отрезка MN, то
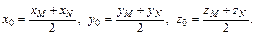
Зная координаты точек О и М, найдем N(4, 1, –3).
2-й способ. Для решения можно также воспользоваться следующими рассуждениями: точка N, симметричная точке M, находится в той же плоскости, что прямая AB и точка M, лежит на перпендикуляре MN к прямой AB и удалена от прямой AB на то же расстояние, что и точка M.
Пусть 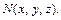 Тогда
Тогда
1) 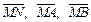 – компланарны;
– компланарны;
2) 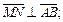
3) 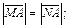
4) середина отрезка MN лежит на прямой AB.
Составим систему уравнений, используя координатную форму записи условий 1–3:
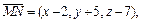
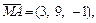
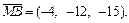
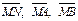 компланарны при условии
компланарны при условии 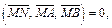 т. е.
т. е. 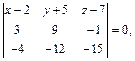 откуда получаем:
откуда получаем:
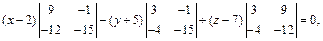
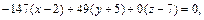 т. е.
т. е.
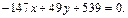
После сокращения имеем:
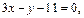 откуда
откуда
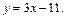 (15.20)
(15.20)
Условие 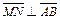 равносильно условию
равносильно условию 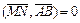 или
или 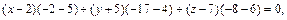 что приводит к уравнению
что приводит к уравнению
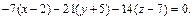
После преобразования имеем:
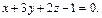
Далее получим:
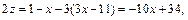
откуда
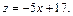 (15.21)
(15.21)
Вычислим:
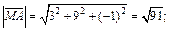
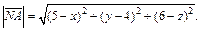
Равенство этих величин дает нам:
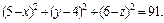
Подставим в последнее равенство правые части формул (15.20) и (15.21) вместо y и z соответственно, откуда получим уравнение 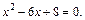
Решим это уравнение, найдя корни 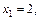
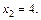
Соответствующие значения y, z вычислим, используя равенства (15.20) и (15.21). Получим точки 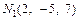 и
и 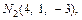 которые удовлетворяют первым трем условиям. Осталось проверить четвертое условие. Найдем середины О1 и О2 отрезков
которые удовлетворяют первым трем условиям. Осталось проверить четвертое условие. Найдем середины О1 и О2 отрезков 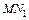 и
и 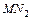 соответственно:
соответственно:
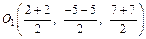 или
или 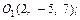
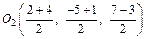 или
или 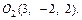
Проверим, какая из точек (О1 или О2) лежит на прямой АВ:
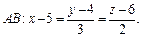
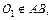 так как
так как 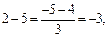 но
но 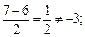
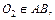 так как
так как 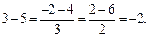
Приходим к ответу: 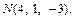
Пример 4. Прямая L задана как линия пересечения плоскостей
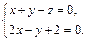
Написать уравнение ее проекции на координатную плоскость Oxz.
Решение. Построим канонические уравнения прямой L. В качестве направляющего вектора можно взять вектор 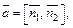 где
где 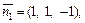
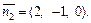 Тогда
Тогда
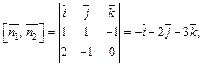 т. е.
т. е. 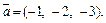
Если 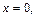 то получим систему уравнений
то получим систему уравнений
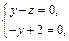
из которой найдем 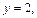
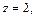 а значит точка
а значит точка 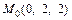 лежит на прямой L.
лежит на прямой L.
Таким образом, канонические уравнения прямой L таковы:
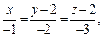
что эквивалентно системе трех уравнений, описывающих три плоскости, проектирующие прямую на координатные плоскости Oxy, Oxz и Oyz соответственно:
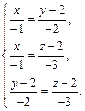
После упрощения получаем:
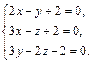
Искомое уравнение: 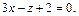
Дата добавления: 2015-09-29; просмотров: 6125;
