Свойства предела функции в точке
1. Если функция f(x) имеет предел в точке х0, то существует окрестность этой точки (за исключением, быть может, самой точки х0), на которой функция ограничена.
2. Если существует предел функции f(x) в точке х0, равный числу 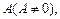 то существует такая окрестность точки х0, на которой функция имеет тот же знак, что и число А.
то существует такая окрестность точки х0, на которой функция имеет тот же знак, что и число А.
3. Если функции f(x) и g(x) имеют пределы в точке х0, то:
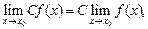 где
где 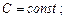
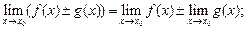 (16.3)
(16.3)
 (16.4)
(16.4)
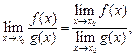 (16.5)
(16.5)
где 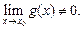
Формулы (16.3) и (16.4) обобщаются на любое конечное количество слагаемых и множителей. В случае их бесконечного количества равенство выполняется не всегда.
Аналогичные свойства верны и для предела функции на бесконечности.
Если в результате непосредственного использования формул (16.3) – (16.5) возникают неопределенности типа 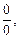
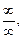
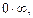
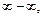 то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей
то вначале необходимо тождественно преобразовать выражение, стоящее под знаком предела (то же для неопределенностей 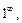
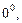
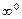 ).
).
Дата добавления: 2015-09-29; просмотров: 1125;
