Второй замечательный предел
 (16.8)
(16.8)
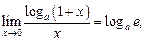 (16.9)
(16.9)
в частности,

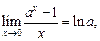 (16.10)
(16.10)
в частности,

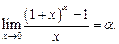 (16.11)
(16.11)
Указанные формулы (16.7) – (16.11) замечательных пределов обобщаются на любую функцию u(x), стоящую вместо независимой переменной х при условии, что 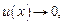 если
если 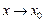 (или
(или  ) во всех формулах, кроме (16.8), в которых
) во всех формулах, кроме (16.8), в которых 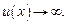
Обобщенная таблица замечательных пределов
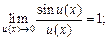
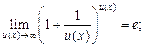
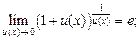 (16.12)
(16.12)
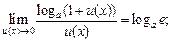
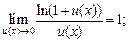 (16.13)
(16.13)
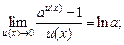
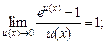 (16.14)
(16.14)
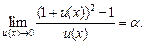 (16.15)
(16.15)
При использовании обобщенных формул на практике вместо 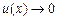
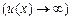 под знаком предела пишут указанное в условии:
под знаком предела пишут указанное в условии: 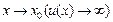 .
.
Все приведенные формулы обобщенной таблицы замечательных пределов (кроме формул (16.12)) раскрывают неопределенность вида 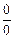 . Формулы (16.12) раскрывают неопределенность вида
. Формулы (16.12) раскрывают неопределенность вида 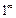 .
.
Пример 1.Вычислить предел функций в точке:
1) 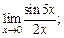 2)
2) 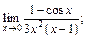 3)
3) 
Решение. 1) При непосредственной подстановке в функцию значения 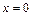 получаем неопределенность вида
получаем неопределенность вида 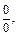 для раскрытия которой воспользуемся первым замечательным пределом:
для раскрытия которой воспользуемся первым замечательным пределом:
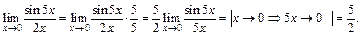
2) При 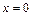 получаем неопределенность вида
получаем неопределенность вида 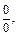 для раскрытия которой сначала применим формулы тригонометрии, а затем первый замечательный предел:
для раскрытия которой сначала применим формулы тригонометрии, а затем первый замечательный предел:
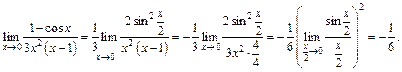
3) Преобразуем вначале разность косинусов в произведение, а затем используем первый замечательный предел:
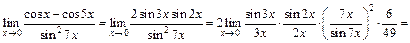
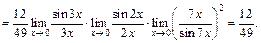
Пример 2. Вычислить предел функции, используя соответствующий замечательный предел:
1) 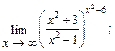 2)
2) 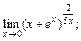
3) 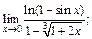 4)
4) 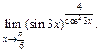
Решение. 1) Воспользуемся первой формулой из (16.12):
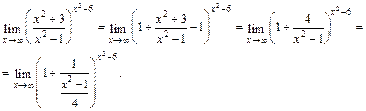
В данном случае 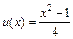 и
и 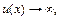 если
если 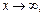 значит
значит
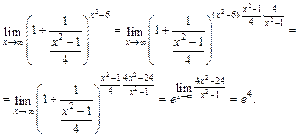
2) Непосредственная подстановка в функцию значения х = 0 дает неопределенность вида 1¥ для раскрытия которой воспользуемся второй формулой из (16.12). Для этого преобразуем выражение под знаком предела:

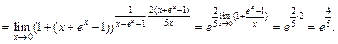
3) При 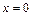 получаем неопределенность вида
получаем неопределенность вида 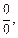 для раскрытия которой сначала упростим выражение, а затем применим формулы (16.7), (16.13), (16.15):
для раскрытия которой сначала упростим выражение, а затем применим формулы (16.7), (16.13), (16.15):
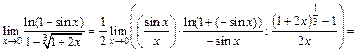
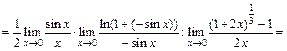
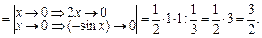
4) Имеем неопределенность вида 1¥. Сделаем замену переменной. Пусть 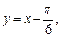 тогда
тогда 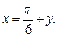 При
При 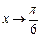 новая переменная
новая переменная 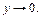 При этом
При этом 
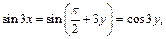 а
а 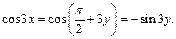
Подставив полученные выражения в формулу, получим:
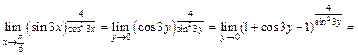
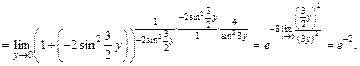
Заметим, что этот пример также можно было решать без замены переменной.
Дата добавления: 2015-09-29; просмотров: 877;
