Графика функции
Левой (правой) полуокрестностью точки х0 называется произвольный интервал 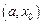
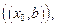 где
где 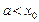
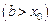 слева (справа).
слева (справа).
Число А называется пределом слева (справа) функции f(x) в точкех0, если функция f(x) определена в некоторой левой (правой) полуокрестности точки 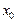 и если для любого
и если для любого 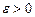 существует
существует 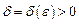 такое, что для всех x, удовлетворяющих условию
такое, что для всех x, удовлетворяющих условию  выполняется неравенство
выполняется неравенство

В этом случае пишут: 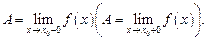
Пределы слева и справа называются односторонними пределами. Если 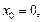 то односторонние пределы обозначают
то односторонние пределы обозначают 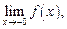
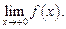
Функция f(x) имеет предел в точке 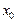 тогда и только тогда, когда в этой точке существуют оба односторонних предела, равных между собой.
тогда и только тогда, когда в этой точке существуют оба односторонних предела, равных между собой.
В этом случае их общее значение является пределом функции f(x) в точке 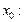
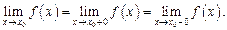
Асимптота графика функции 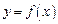 – это прямая линия, к которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.
– это прямая линия, к которой неограниченно приближается график данной функции, когда его точка неограниченно удаляется от начала координат.
Различают горизонтальную, вертикальную и наклонную асимптоты.
Прямая 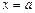 называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 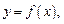 если
если 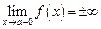 или
или 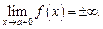
В случае вертикальной асимптоты 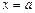 функция является бесконечно большой в точке
функция является бесконечно большой в точке 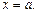
Прямая y = b называется горизонтальной асимптотой графика функции 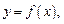 если
если 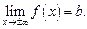
Вертикальные асимптоты могут существовать у функций, которые определены не на всей числовой прямой, т. е. имеют разрыв второго рода.
Если областью определения функции является вся числовая прямая, то у функции нет вертикальных асимптот.
Прямая 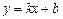 называется наклонной асимптотой графика функции
называется наклонной асимптотой графика функции 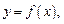 при
при 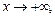 если
если
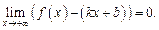
Для нахождения коэффициентов k и b применяют следующие формулы:
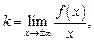 (16.25)
(16.25)
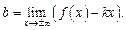 (16.26)
(16.26)
Если хотя бы один из пределов (16.25), (16.26) равен 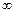 или не существует, то у функции наклонных асимптот нет.
или не существует, то у функции наклонных асимптот нет.
Если 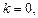
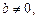 то прямая
то прямая 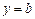 является горизонтальной асимптотой. Заметим, что наклонных асимптот у функции может быть не больше двух, а вертикальных может быть сколько угодно.
является горизонтальной асимптотой. Заметим, что наклонных асимптот у функции может быть не больше двух, а вертикальных может быть сколько угодно.
Пример 1. Найти односторонние пределы функции f(x) в точке х0:
1) 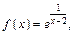
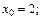 2)
2) 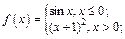
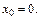
Решение.1) Вычислим пределы функции в точке 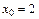 слева и справа, т. е.
слева и справа, т. е. 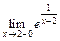 и
и 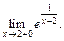
Если 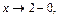 то
то 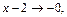 значит
значит 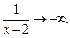 Получаем
Получаем 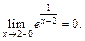
Если 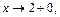 то
то 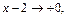 значит
значит  Получаем
Получаем 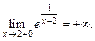
2) При 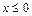 функция задана формулой
функция задана формулой 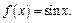 Поэтому
Поэтому
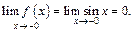
При  функция задана формулой
функция задана формулой 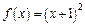 т. е.
т. е.
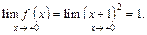
Значит 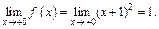
Пример 2.С помощью односторонних пределов показать, что функция  не имеет предела в точке
не имеет предела в точке 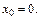
Решение. При 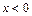 имеем
имеем 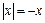 и функция принимает вид:
и функция принимает вид:
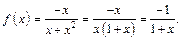
Поэтому 
При  имеем
имеем  и функцию
и функцию 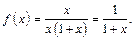
Поэтому 
Получим, что оба односторонних предела функции в точке 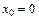 существуют, однако они различны, поэтому
существуют, однако они различны, поэтому 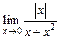 не существует.
не существует.
Пример 3.Найти асимптоты графика функции:
1) 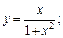 2)
2) 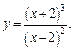
Решение. 1)Вертикальных асимптот данная функция не имеет, потому что она определена для любых 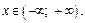 Для того чтобы найти горизонтальные асимптоты, надо рассмотреть пределы функции на бесконечности:
Для того чтобы найти горизонтальные асимптоты, надо рассмотреть пределы функции на бесконечности:
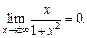
Получили, что 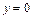 – горизонтальная асимптота (ось 0x).
– горизонтальная асимптота (ось 0x).
Будем искать наклонные асимптоты в виде функции 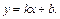
Согласно формулам (16.25) и (16.26), вычисляем:
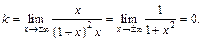
Так как  значит наклонных асимптот у графика нет.
значит наклонных асимптот у графика нет.
2) Так как при 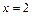 функция не определена, рассмотрим
функция не определена, рассмотрим
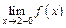 и
и 
Вычисляем:
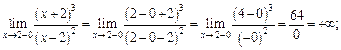
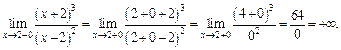
Поэтому прямая 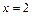 является вертикальной асимптотой графика функции.
является вертикальной асимптотой графика функции.
Ищем горизонтальную асимптоту.
Вычисляем
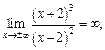
это означает, что горизонтальных асимптот нет.
Выясним наличие наклонных асимптот. По формулам (16.25) и (16.26) находим:
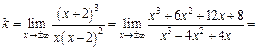
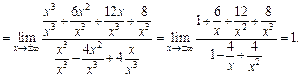
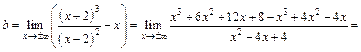
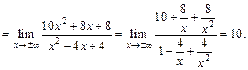
Приходим к выводу, что 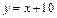 – наклонная асимптота.
– наклонная асимптота.
Пример 4.Найти асимптоты графика функции:
1) 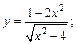 2)
2) 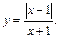
Решение. 1) Областью определения D(y) функции является то множество, на котором выполняется неравенство 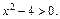 Решив последнее неравенство, получим что
Решив последнее неравенство, получим что 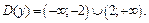
Определим вертикальные асимптоты графика функции. Рассмотрим поведение функции в окрестности точки 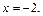 Функция определена только в левой полуокрестности этой точки, поэтому вычисляем левосторонний предел:
Функция определена только в левой полуокрестности этой точки, поэтому вычисляем левосторонний предел:
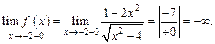
В окрестности точки 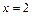 функция определена только справа, поэтому в этой точке можем рассмотреть правосторонний предел:
функция определена только справа, поэтому в этой точке можем рассмотреть правосторонний предел:
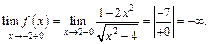 .
.
Приходим к заключению, что прямые 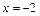 и
и 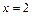 являются вертикальными асимптотами графика функции. Горизонтальных асимптот нет, так как
являются вертикальными асимптотами графика функции. Горизонтальных асимптот нет, так как
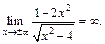
Найдем наклонные асимптоты:
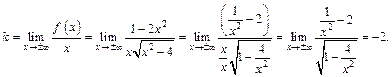
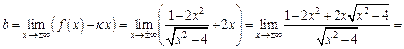
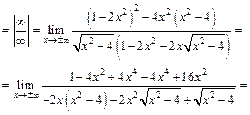
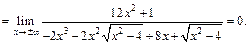
Таким образом, 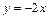 – наклонная асимптота.
– наклонная асимптота.
2) Функция определена всюду на числовой прямой, кроме точки 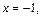 т. е.
т. е. 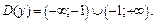 Рассмотрим
Рассмотрим
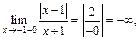
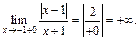
Прямая 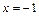 – вертикальная асимптота.
– вертикальная асимптота.
Найдем горизонтальные асимптоты:
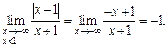

Получаем, что прямая 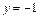 является горизонтальной асимптотой при
является горизонтальной асимптотой при 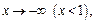 а прямая
а прямая 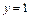 – горизонтальная асимптота при
– горизонтальная асимптота при 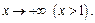
Ищем наклонные асимптоты:
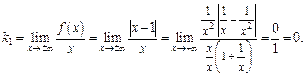
Наклонных асимптот нет.
Дата добавления: 2015-09-29; просмотров: 2176;
