Точек разрыва

Функция f(x) называется непрерывной в точке 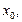если она определена в этой точке и некоторой ее окрестности и если выполняется условие

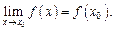(16.27)

Если функция 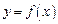непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна на этом промежутке.

Существуют и другие определения непрерывности функции в точке. Функция f(x) называется непрерывной в точке, если она определена в этой точке и некоторой ее окрестности и если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции в этой точке:

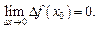(16.28)

Непрерывность функции в точке определяется также на основе односторонних пределов.

Функция f(x) называется непрерывной в точке 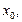если она определена в этой точке и некоторой ее окрестности и если существуют односторонние пределы (конечные) такие, что

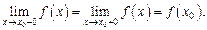(16.29)