Свойства непрерывных функций. 1. Если функции f(x) и g(x) непрерывны в точке х0, то их сумма также есть непрерывная функция в точке х0

1. Если функции f(x) и g(x) непрерывны в точке х₀, то их сумма 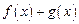также есть непрерывная функция в точке х₀. Это свойство справедливо для любого конечного количества слагаемых.

2. Произведение конечного количества непрерывных функций есть функция непрерывная.

3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

4. Если функция f(x) непрерывна в точке х₀ и 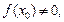то значения функции f(x) в некоторой окрестности точки х₀ имеют тот же знак, что и функция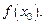

5. Если функция 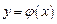непрерывна в точке х₀ и принимает в этой точке значение 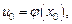а функция f(u) непрерывна в точке 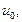то сложная функция 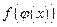в точке х₀ непрерывна.

6. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.

7. Если непрерывная на некотором отрезке функция f(x) принимает на его концах значения разных знаков, то на этом отрезке найдется хотя бы одна точка, в которой функция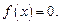

8. Если функция f(x) непрерывна в точке х₀, то операции вычисления предела в этой точке и функции f переставимы, т. е.

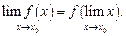(16.30)

На свойстве 8 (равенство (16.30)) и было основано непосредственное вычисление предела функции в случае отсутствия неопределенности (см. § 16.1–16.4).

Если нарушается хотя бы одно условие, указанное в определении непрерывности, то точка х₀ называется точкой разрывафункции.

Классификацию точек разрыва дают в зависимости от того, какое условие последнего определения непрерывности, в том числе равенства (16.29), нарушено.