Свойства проекции вектора на ось
1. 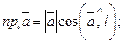
2. 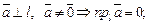
3. 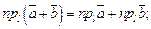
4. 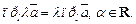
Скалярное произведение двух векторов в пространстве определяется аналогично случаю на плоскости:
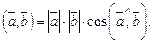
Формула скалярного квадрата:
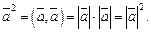
Справедлива формула, связывающая скалярное произведение векторов и проекции этих векторов:
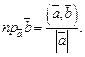 (14.1)
(14.1)
Пример 1. Дана треугольная призма  (рис. 14.3). Разложить вектор
(рис. 14.3). Разложить вектор 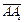 по векторам
по векторам 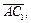
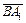 и
и 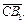
Решение. По правилу треугольника имеем:
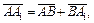
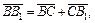
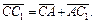
Складывая левые и правые части этих векторных равенств, получаем:
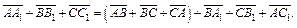
Так как 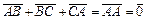 и
и 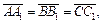 то
то 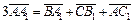 и, следовательно,
и, следовательно, 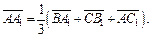

Рис. 14.3
Пример 2. При соблюдении каких условий ненулевые векторы 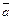 и
и 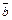 удовлетворяют условию
удовлетворяют условию 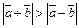 ?
?
Решение. Так как неравенство связывает неотрицательные числовые величины, возведем в квадрат, что не изменит его смысла:
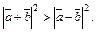
Перейдя к скалярному квадрату и воспользовавшись алгебраическими свойствами скалярного произведения, получим:
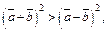
откуда
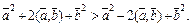
Получаем:
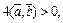 т. е.
т. е. 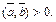
Очевидно, последнее условие выполняется при 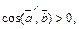 т. е. при
т. е. при 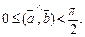
Таким образом, векторы или сонаправлены 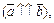 или образуют острый угол.
или образуют острый угол.
Пример 3. Вычислить 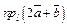 и
и 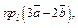 если
если 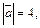
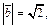 а векторы
а векторы 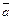 и
и 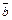 образуют с осью l соответственно углы в 120° и 45°.
образуют с осью l соответственно углы в 120° и 45°.
Решение. Согласно свойствам проекции, имеем:
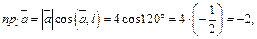
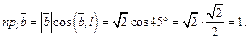
Тогда получаем:
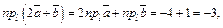
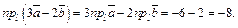
Пример 4. Найти проекцию вектора 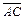 на направление вектора
на направление вектора 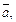 если
если 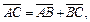
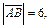
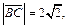
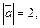
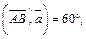
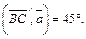
Решение. Используем свойства проекции:
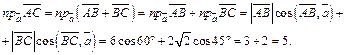
Пример 5. Вычислить длины диагоналей параллелограмма, построенного на векторах 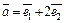 и
и 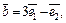 если
если 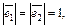
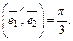
Решение. Пусть 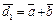 и
и 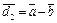 . Тогда
. Тогда 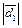 и
и 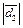 представляют длины диагоналей параллелограмма, построенного на векторах
представляют длины диагоналей параллелограмма, построенного на векторах 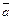 и
и 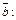
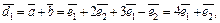
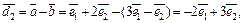
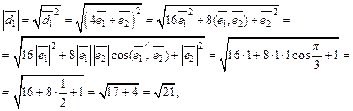
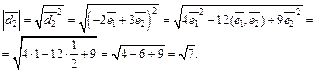
Пример 6. Найти угол между векторами 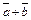 и
и 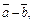 если
если 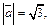
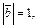
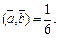
Решение. Обозначим угол между векторами φ, тогда
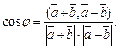
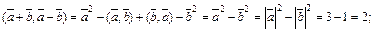
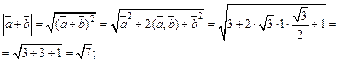
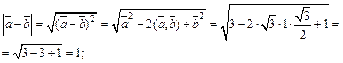
Тогда 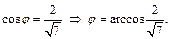
Дата добавления: 2015-09-29; просмотров: 758;
