Обратная матрица. Ранг матрицы

Квадратная матрица B, удовлетворяющая совместно с заданной матрицей A того же порядка равенствам 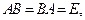называется обратной к матрице A и обозначается A^–1. Обратная матрица A^–1 существует при условии, что A – невырожденная матрица, т. е.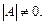

Обратную матрицу можно вычислить следующими способами:

1-й способ. Используют формулу

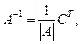(13.4)

где С – матрица, составленная из алгебраических дополнений соответствующих элементов матрицы A.

2-й способ. Для данной матрицы A n-го порядка строится прямоугольная матрица 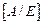размера 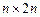путем приписывания к матрице A справа единичной матрицы n-го порядка, затем с помощью элементарных преобразований над строками матрица 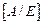приводится к виду 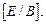Тогда

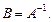
Рангом матрицы A размера 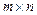называется максимальный порядок r_A отличных от нуля ее миноров. При этом под минором k-го порядка матрицы понимают определитель, составленный из элементов матрицы A, стоящих на пересечении k ее строк и k столбцов. Любой ненулевой минор порядка r называется базисным минором матрицы A.