Основные методы вычисления определителей
1. Для определителей 3-го порядка используют правило треугольников, которое схематично можно изобразить следующим образом:

Линии соединяют по три элемента, которые умножаются, а затем произведения складываются.
2. Определитель порядка n может быть вычислен разложением по любой строке (столбцу):
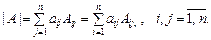
3. Метод эффективного понижения порядка определителя: используя свойства определителя, его преобразуют к такому виду, чтобы все элементы некоторой строки (столбца) определителя, кроме одного, стали нулевыми, затем вычисляют определитель разложением по этой строке (столбцу).
4. Метод приведения к треугольномуили диагональному виду с использованием свойств определителя, когда определитель равен произведению диагональных элементов.
Пример 1.Вычислить определитель 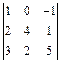 различными способами.
различными способами.
Решение. 1-й способ. Используем правило треугольников:
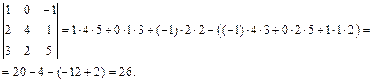
2-й способ. Разложим определитель по первой строке:
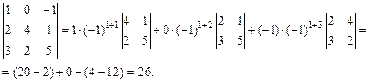
3-й способ. Занулим элементы первой строки, т. е. используем метод эффективного понижения порядка. Для этого прибавим к элементам 3-го столбца элементы 1-го столбца. Затем разложим определитель по 1-й строке:
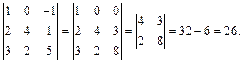
4-й способ. Используя свойства определителя, приведем его к треугольному виду:
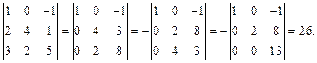
Пример 2.Вычислить определитель 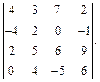
Решение. Используем метод эффективного понижения порядка. Для этого из первой строки вычтем, а ко второй прибавим удвоенную третью строку. Полученный определитель разложим по первому столбцу:
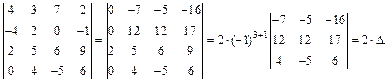
Далее, ко второму столбцу определителя Δ прибавим третий столбец, после чего преобразуем следующим образом: прибавим к первому и третьему столбцам второй столбец, умноженный соответственно на –4 и на –6. В результате получим:
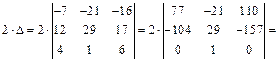
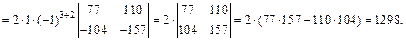
Пример 3.Выяснить, при каких условиях определитель 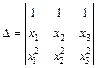 не равен нулю.
не равен нулю.
Решение. Разложим определитель по 3-й строке:
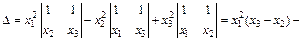
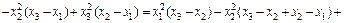
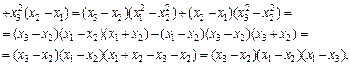
Значит, 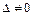 , при
, при 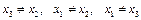 .
.
Пример 4. Доказать равенство
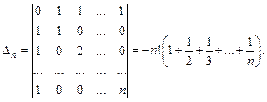
Решение. Для доказательства используем метод математической индукции. Проверим справедливость утверждения при n = 1 и 2.
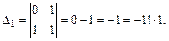
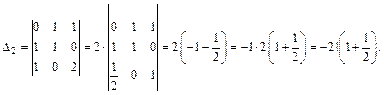
Пусть равенство выполняется при n = k, где k > 2, т. е. 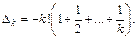 Докажем истинность при n = k + 1.
Докажем истинность при n = k + 1.
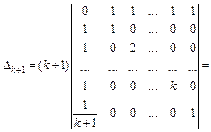
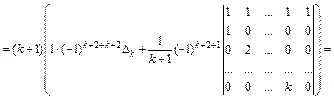
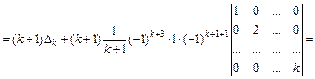
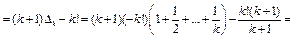
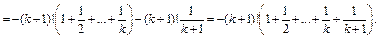
Утверждение доказано методом математической индукции.
Пример 5.Вычислить определитель:
1) 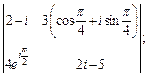
2) 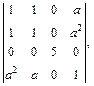 где
где 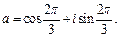
Решение. 1) Перейдем к алгебраической форме записи всех элементов заданной матрицы: 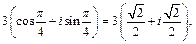
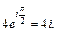 Тогда
Тогда
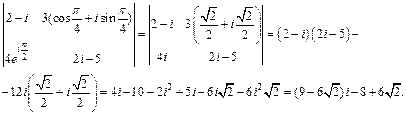
2) Вычислим определитель разложением по третьему столбцу:
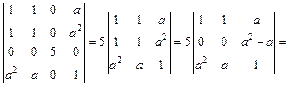
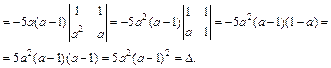
Поскольку 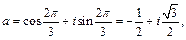 то
то 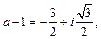
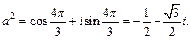 Значит,
Значит,
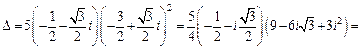
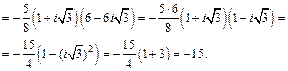
Дата добавления: 2015-09-29; просмотров: 1805;
