Уравнение с разделяющимися переменными
Этот тип уравнения является самым простым типом уравнений первого порядка.
Дифференциальное уравнение вида
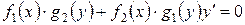
называется уравнением с разделяющимися переменными.
Представим производную как отношение дифференциалов 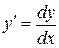 , тогда
, тогда
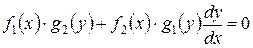 .
.
Умножаем на 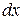
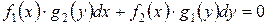 .
.
Разделение переменных производится делением обеих частей последнего соотношения на произведение 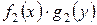 , в котором
, в котором 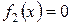 ,
, 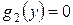 . После деления уравнение примет вид
. После деления уравнение примет вид
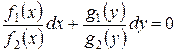 или
или 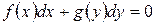 ,
,
а его общий интеграл запишется так:
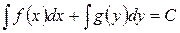 или
или  .
.
Пример. Решить уравнение 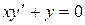 .
.
Решение. Подставим вместо 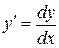
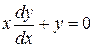 .
. 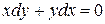 .
.
Разделим на 
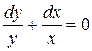 .
.
Интегрируя, получим
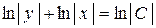 .
.
Здесь удобно представить константу в логарифмической форме. Из последнего равенства получим
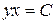 ;
; 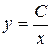 .
.
Дата добавления: 2015-09-28; просмотров: 564;
