Основные свойства определенного интеграла. 1о Значение определенного интеграла не зависит от переменной интегрирования . 2о Если пределы интегрирования поменять местами
| 1о | Значение определенного интеграла не зависит от переменной интегрирования
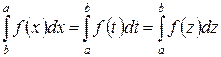 . .
|
| 2о | Если пределы интегрирования поменять местами, то интеграл изменит знак на противоположный
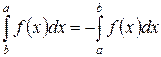 . .
|
| 3о | Интеграл с одинаковыми пределами интегрирования равен нулю
 . .
|
| 4о | Если отрезок интегрирования разбить точкой 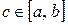 , то интеграл по всему отрезку , то интеграл по всему отрезку 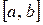 будет равен сумме интегралов по его частям будет равен сумме интегралов по его частям
 .
Формула оказывается верной для любого расположения точек .
Формула оказывается верной для любого расположения точек 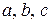 при условии существования всех входящих в нее интегралов. при условии существования всех входящих в нее интегралов.
|
| 5о | Интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме интегралов от этих функций
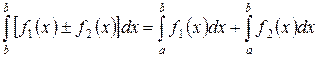 . .
|
| 6о | Постоянный множитель можно выносить за знак интеграла

|
| 7о | Определенный интеграл в симметричных относительно нуля пределах 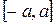 от четной функции равен удвоенному интегралу на половине интервала интегрирования: от четной функции равен удвоенному интегралу на половине интервала интегрирования:
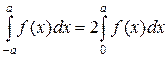
|
| 8о | Определенный интеграл в симметричных относительно нуля пределах 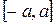 от нечетной функции равен нулю от нечетной функции равен нулю

|
Дата добавления: 2015-09-28; просмотров: 682;
