Понятие определенного интеграла. Пусть функция определена и непрерывна на отрезке
Пусть функция 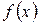 определена и непрерывна на отрезке
определена и непрерывна на отрезке 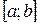 . Разделим отрезок
. Разделим отрезок 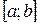 на
на 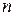 произвольных частей точками
произвольных частей точками 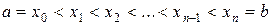 , выберем на каждом элементарном отрезке
, выберем на каждом элементарном отрезке 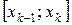 произвольную точку
произвольную точку 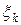 и найдем длину каждого такого отрезка:
и найдем длину каждого такого отрезка: 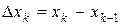 .
.
Интегральной суммой для функции 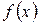 на отрезке
на отрезке 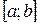 называется сумма вида
называется сумма вида
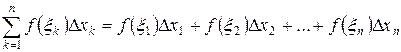 .
.
Для каждой непрерывной на 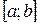 функции
функции 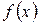 можно построить бесконечное число интегральных сумм, каждая из которых зависит от разбиения отрезка
можно построить бесконечное число интегральных сумм, каждая из которых зависит от разбиения отрезка 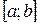 на части и выбора точек
на части и выбора точек 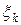 на каждом элементарном отрезке.
на каждом элементарном отрезке.
| Определение. | Определенным интегралом от функции 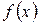 на отрезке на отрезке 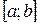 называется предел интегральных сумм при условии, что длина наибольшего из элементарных отрезков стремится к нулю; если этот предел существует и не зависит от способа разбиения отрезка называется предел интегральных сумм при условии, что длина наибольшего из элементарных отрезков стремится к нулю; если этот предел существует и не зависит от способа разбиения отрезка 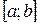 на части и выбора точек на части и выбора точек 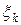 на каждом из элементарных отрезков: на каждом из элементарных отрезков:
|
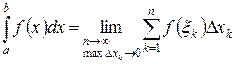 .
.
Числа 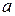 и
и 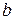 называют пределами интегрирования;
называют пределами интегрирования; 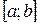 – отрезком интегрирования;
– отрезком интегрирования; 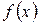 – подынтегральной функцией;
– подынтегральной функцией; 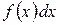 – подынтегральным выражением;
– подынтегральным выражением; 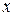 – переменной интегрирования.
– переменной интегрирования.
| Теорема | существования определенного интеграла.
Если функция 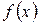 непрерывна на непрерывна на 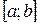 , то предел интегральной суммы существует и не зависит от способа разбиения отрезка , то предел интегральной суммы существует и не зависит от способа разбиения отрезка 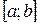 на элементарные и от способа выбора точек на элементарные и от способа выбора точек 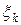 . .
|
Если 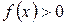 на
на 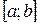 , то определенный интеграл
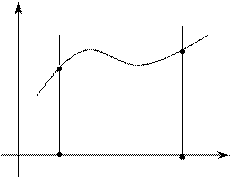
, то определенный интеграл 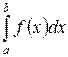 геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями
геометрически представляет собой площадь криволинейной трапеции – фигуры, ограниченной линиями 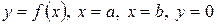 (рис. 10).
(рис. 10).
| 
| |||||||||
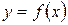
| ||||||||||
0 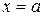 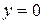 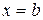 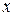
| ||||||||||
| Рис. 10 |
Дата добавления: 2015-09-28; просмотров: 736;
