Интегрирование по частям. Интегрированием по частям называется нахождение интеграла по формуле:
Интегрированием по частям называется нахождение интеграла по формуле:
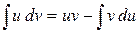 ,
,
где 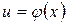 ,
, 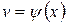 – непрерывно дифференцируемые функции от
– непрерывно дифференцируемые функции от 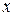 .
.
С помощью этой формулы нахождение интеграла 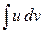 сводится к отысканию другого интеграла
сводится к отысканию другого интеграла 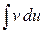 . Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
. Ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.
При этом через 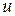 обозначают такую функцию, которая при дифференцировании упрощается, а через
обозначают такую функцию, которая при дифференцировании упрощается, а через 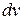 – ту часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например, для интегралов
– ту часть подынтегрального выражения, интеграл от которой известен или может быть найден. Так, например, для интегралов 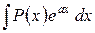 ,
, 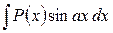 ,
, 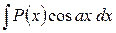 , где
, где 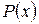 – многочлен, за
– многочлен, за 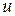 следует принять
следует принять 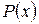 , а за
, а за 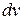 – соответственно выражения
– соответственно выражения 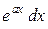 ,
, 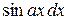 ,
, 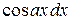 .
.
Для интегралов вида 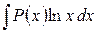 ,
, 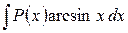 ,
, 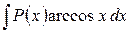 ,
, 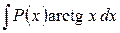 ,
, 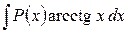 за
за 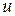 принимают соответственно функции
принимают соответственно функции 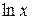 ,
, 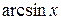 ,
, 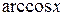 ,
, 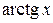 ,
, 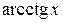 а за
а за 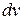 – выражение
– выражение 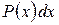 .
.
Пример. Найти интеграл 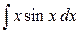 .
.
Решение.
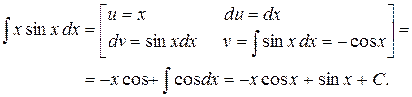
Пример. Найти интеграл 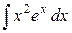 .
.
Решение.
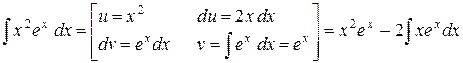 .
.
Мы добились понижения степени 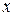 на единицу. Чтобы найти
на единицу. Чтобы найти 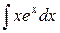 , применим еще раз интегрирование по частям:
, применим еще раз интегрирование по частям:
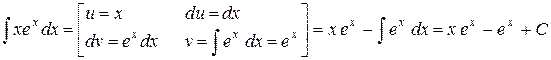 .
.
Окончательно имеем:
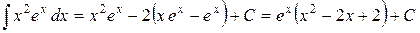 .
.
Дата добавления: 2015-09-28; просмотров: 735;
