Обчислення. Приклад 8. Молот масою 70 кг падає з висоти 5 м і вдаряє по залізній поковці, що лежить на ковадлі
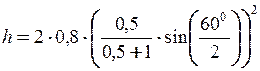 = 0,044 м.
= 0,044 м.
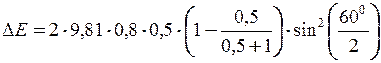 =1,3 Дж.
=1,3 Дж.
Відповідь:h = 0,044 м; ∆E = 1,3 Дж.
Приклад 8. Молот масою 70 кг падає з висоти 5 м і вдаряє по залізній поковці, що лежить на ковадлі. Маса кувалди разом з поковкою 1330 кг. Вважаючи удар абсолютно непружним, визначити енергію, що витрачається на деформацію виробу. Систему молот-поковка-ковадло вважати замкненою.
Дано: m1 = 70 кг, m2 =1330 кг; h = 5 м.
Знайти: EД.
Розв’язок. За умовою задачі система молот-поковка-ковадла вважається замкненою, а удар непружний. На підставі закону збереження енергії можна вважати, що енергія, витрачена на деформацію поковки, дорівнює різниці значень механічної енергії системи до і після удару.
Вважаємо, що під час удару змінюється тільки кінетична енергія тіл, тобто незначним переміщенням тіл по вертикалі під час удару нехтуємо. Тоді для енергії деформації виробу маємо
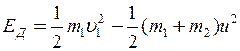 , (1)
, (1)
де u – загальна швидкість усіх тіл системи після непружного удару, а  – швидкість молота наприкінці падіння з висоти h.
– швидкість молота наприкінці падіння з висоти h.
Швидкість  легко знайти, тому що початкова потенціальна енергія молота (на висоті h) дорівнює його кінетичній енергії безпосередньо перед ударом об поковку
легко знайти, тому що початкова потенціальна енергія молота (на висоті h) дорівнює його кінетичній енергії безпосередньо перед ударом об поковку
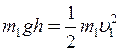 . (2)
. (2)
Зауважимо, що для даної системи виконується закон збереження імпульсу
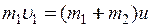 . (3)
. (3)
З виразу (2) можна знайти швидкість  , а потім з виразу (3) – швидкість u
, а потім з виразу (3) – швидкість u
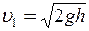 ; (4а)
; (4а)
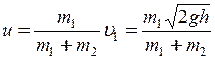 . (4б)
. (4б)
Підставляючи вираження (4) у (1), тепер легко одержати остаточну формулу
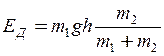 .
.
Дата добавления: 2015-09-28; просмотров: 848;
