Обчислення. Приклад 2. Два точкові електричні заряди 1 нКл і –2 нКл знаходяться у повітрі на відстані 10 см один від одного
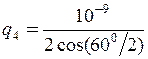 = 5,77·10-9 Кл.
= 5,77·10-9 Кл.
Відповідь:q4 = 5,77·10-9 Кл.
Приклад 2. Два точкові електричні заряди 1 нКл і –2 нКл знаходяться у повітрі на відстані 10 см один від одного. Визначити напруженість і потенціал електричного поля, створюваного цими зарядами, у точці, віддаленій від першого заряду на 9 см і від другого – на 7 см.
Дано: q1= 10-9 Кл; q2= –2·10-9 Кл; d = 0,1 м; r1= 9·10-2 м; r2= 7·10-2 м.
Знайти: E; 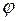 .
.
Розв’язок. Відповідно до принципу суперпозиції, напруженість електричного поля 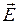 в пошукуваній точці дорівнює векторній сумі полів
в пошукуваній точці дорівнює векторній сумі полів  і
і  , створених кожним зарядом q1 і q2 окремо
, створених кожним зарядом q1 і q2 окремо
 , (1)
, (1)
де
 ; (2а)
; (2а)
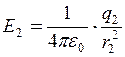 . (2б)
. (2б)
Вектор  (рис. 3.2) спрямований уздовж силової лінії від заряду
(рис. 3.2) спрямований уздовж силової лінії від заряду
q1, оскільки цей заряд позитивний; вектор  спрямований за силовою лінії до заряду q2, тому що цей заряд негативний. Модуль результуючого вектора спрямований за силовою лінії до заряду q2, тому що цей заряд негативний. Модуль результуючого вектора 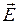 знайдемо за теоремою косинусів знайдемо за теоремою косинусів
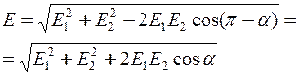 . (3) . (3)
| 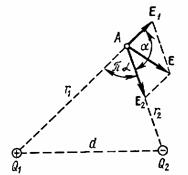 Рис. 3.2.
Рис. 3.2.
|
Тут  – кут між векторами
– кут між векторами  і
і  , що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r1 і r2
, що може бути також визначений за теоремою косинусів із трикутника, утвореного сторонами d, r1 і r2
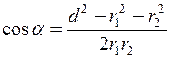 . (4)
. (4)
Підставляючи в (3) вираз (2) і (4), одержимо
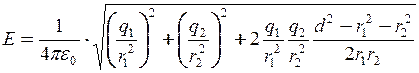 . (5)
. (5)
Потенціал результуючого поля, відповідно до принципу суперпозиції, дорівнює алгебраїчній сумі потенціалів
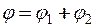 . (6)
. (6)
Тут  і
і  – потенціали полів точкових зарядів q1 і q2 у пошукуваній точці
– потенціали полів точкових зарядів q1 і q2 у пошукуваній точці
 ; (7а)
; (7а)
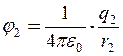 . (7б)
. (7б)
Таким чином, з (6) і (7) одержимо
 , (8)
, (8)
де варто враховувати знаки зарядів q1 і q2.
При обчисленнях візьмемо до уваги, що в одиницях СІ загальний множник виразів (5) і (8) дорівнює
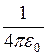 = 9·109 м/Ф.
= 9·109 м/Ф.
Обчислення.
 = 3,58·103 В/м;
= 3,58·103 В/м;
 В.
В.
Відповідь: E = 3,58·103 В/м; 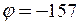 В.
В.
Приклад 3. Уздовж тонкого кільця рівномірно розподілений заряд у 40 нКл з лінійною густиною 50 нКл/м. Визначити напруженість електричного поля, створеного цим зарядом у точці, що лежить на осі кільця і віддалена від його центра на відстань, що дорівнює половині радіуса.
Дано: q = 4·10-8 Кл;  = 5·10-8 Кл/м; h = R/2.
= 5·10-8 Кл/м; h = R/2.
Знайти: E.
Розв’язок. Виділимо на кільці малу ділянку довжиною dl (рис. 3.3). Оскільки заряд dq1 =  dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля dl, який знаходиться на цій ділянці, вважається точковим, то напруженість електричного поля 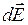 , що створено цим зарядом, можна записати у вид , що створено цим зарядом, можна записати у вид
 . (1) . (1)
| 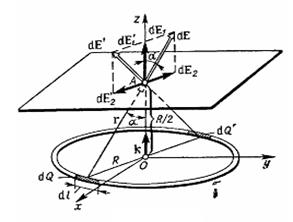 Рис. 3.3.
Рис. 3.3.
|
Розкладемо вектор 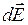 на дві складові:
на дві складові: 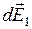 , перпендикулярну площини кільця, і
, перпендикулярну площини кільця, і  , паралельну до площини кільця, тобто
, паралельну до площини кільця, тобто
 . (2)
. (2)
Напруженість E електричного поля в пошукуваній точці знайдемо інтегруванням
 ,
,
де інтегрування ведеться по всіх елементах зарядженого кільця. З рисунка бачимо, що для кожної пари зарядів dq і dq′, розташованих симетрично щодо центра кільця, складові  і
і  однакові за модулем і протилежні за напрямком:
однакові за модулем і протилежні за напрямком:  . Тому векторна сума
. Тому векторна сума  . Складові
. Складові 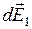 для всіх елементів кільця напрямлені уздовж осі кільця, тому
для всіх елементів кільця напрямлені уздовж осі кільця, тому
 , (3)
, (3)
де  , або з урахуванням (1)
, або з урахуванням (1) 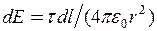 ,
,  ,
, 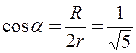 .
.
З урахуванням цього
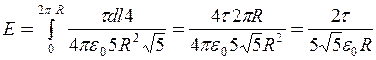 . (4)
. (4)
Із співвідношення 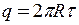 визначимо радіус кільця
визначимо радіус кільця 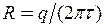 . Тоді
. Тоді
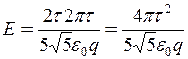 . (5)
. (5)
Зробимо обчислення.
 = 7,92·103 В/м.
= 7,92·103 В/м.
Відповідь: E = 7,92·103 В/м.
Приклад 4. Нескінченна площина, розташована вертикально, заряджена рівномірно з поверхневою густиною заряду 40 мкКл/м2. На шовковій нитці, один з кінців якої закріплений у точці на цій площині, підвішена кулька масою 1 г, що несе заряд 1 нКл. Який кут із площиною утворить нитка, на якій висить кулька?
Дано: 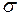 = 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
= 4·10-5 Кл/м2; q = 10-9 Кл; m = 10-3 кг.
Знайти:  .
.
Розв’язок. У стані рівноваги результуюча усіх сил, що діють на кульку (рис. 3.4), дорівнює нулю
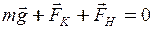 . (1)
. (1)
Тут  , ,  і і 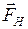 – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки.
Векторна сума взаємно перпендикулярних сил – відповідно сила ваги, сила кулонівського відштовхування і сила натягу нитки.
Векторна сума взаємно перпендикулярних сил  і і  (на рис. 3.4 – сила (на рис. 3.4 – сила  ) спрямована уздовж нитки і в стані рівноваги урівноважується силою ) спрямована уздовж нитки і в стані рівноваги урівноважується силою 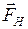 . З цього випливає, що пошукуваний кут дорівнює кутові між векторами . З цього випливає, що пошукуваний кут дорівнює кутові між векторами  і і  , тому , тому
|
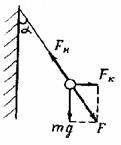 Рис. 3.4.
Рис. 3.4.
|
 . (2)
. (2)
Кулонівська сила, що діє на заряджену кульку в однорідному електричному полі площини, дорівнює
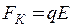 . (3)
. (3)
Тут E – напруженість електричного поля, створювана рівномірно зарядженою площиною
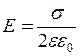 . (4)
. (4)
Таким чином, з (2)–(4) можна одержати остаточний вираз для пошукуваного кута
 . (5)
. (5)
Дата добавления: 2015-09-28; просмотров: 4118;
