Обчислення. Відповідь:M = –1,61 Н; N = 180 оборотів

M = 2·3,14·4·0,4²·(0 – 12)/30 = –1,61 Н;

N = (0 + 12)·30/2 = 180.

Відповідь:M = –1,61 Н; N = 180 оборотів. Знак «–»указує на те, що момент сил гальмуючий.

Приклад 11. Через блок у вигляді суцільного диска, що має масу 80 г (рис. 1.5), перекинуто тонку гнучку нитку, до кінців якої підвішено вантажі з масами 100 г і 200 г. Визначити прискорення, з яким будуть рухатися вантажі, якщо їх полишити н самих себе. Тертям і масою нитки знехтувати. Дано: m = 0,08 кг; m1 = 0,1 кг; m2 = 0,2 кг. Знайти: a.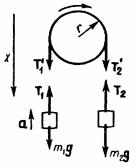

Рис. 1.5.

Розв’язок. Система, що рухається, складається з трьох тіл – двох вантажів і блоку, для яких можна застосувати рівняння руху. Обидва вантажі рухаються поступально, і на кожен діють дві сили: сила ваги і сила натягу нитки. Направивши вісь x вертикально донизу, для кожного вантажу можна записати рівняння руху (рівняння другого закону Ньютона) у проекціях на цю вісь

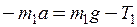; (1)

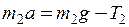. (2)

Блок обертається під дією моментів сил 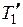і 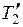щодо осі, перпендикулярної до площини креслення і спрямованої за креслення, у результаті чого він набуває кутове прискорення 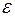, обумовлене рівнянням динаміки обертального руху для твердого тіла

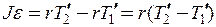, (3)

де J – момент інерції блоку.

Для суцільного диска момент інерції відносно осі, що проходить по осі симетрії, маємо

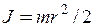. (4)

Лінійне прискорення вантажів чисельно дорівнює тангенціальному прискоренню точок на зовнішній поверхні блоку, тому що відсутнє проковзування нитки. Прискорення a і 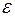зв’язані співвідношенням

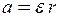. (5)

Нитки, як видно з умови задачі, можна вважати невагомими. Тому, згідно з третім законом Ньютона, відповідні сили дорівнюють

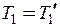; (6а)

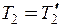. (6б)

Підставляючи вирази (4)-(6) у (3), після нескладних перетворень легко одержати

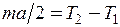. (7)

Рівняння (1), (2) і (7) являють собою систему, що містить три невідомі величини – прискорення a і сили натягу ниток T₁ і T₂. Для її розв’язку можна, наприклад, замінити знаки на протилежні в (1), а потім скласти між собою відповідно ліві і праві частини всіх рівнянь системи. В результаті легко одержати остаточний вираз для пошукуваного прискорення

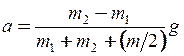. (8)