Обчислення. Приклад 13. Стрижень довжиною 1 м рухається повз спостерігача із швидкістю 0,8c (c – швидкість світла у вакуумі)

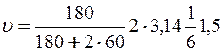= 1 м/с.

Відповідь: = 1 м/с.

Приклад 13. Стрижень довжиною 1 м рухається повз спостерігача із швидкістю 0,8c (c – швидкість світла у вакуумі). Якою буде довжина цього стрижня в системі відліку, пов’язаної зі спостерігачем?

Дано: l₀ = 1 м; = 0,8c.

Знайти: l.

Розв’язок. Залежність довжини тіла від швидкості в релятивістській механіці виражається формулою

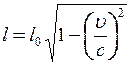. (1)

Підставляючи у формулу (1) числові значення, одержимо

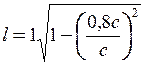= 0,6 м.

Відповідь: l = 0,6 м.

Приклад 14. Дві частинки рухаються назустріч одна одній із швидкостями щодо нерухомого спостерігача: 1) 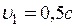; ; 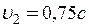2) 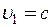; 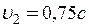. Знайти їхню відносну швидкість у першому і другому випадках.

Дано: 1) 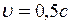; u = 0,75c; 2) 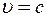, u = 0,75c.

Знайти: u^′.

Розв’язок. Закон додавання швидкостей у релятивістській механіці визначається формулою

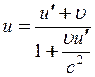, (1)

де u – швидкість частинки в базовій інерціальній системі відліку К, 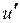– швидкість частинки в інерціальній системі відліку 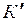, – швидкість системи 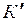щодо системи К. Зважаючи на те, що частинки рухаються на зустріч одна одній, формулу (1) треба записати таким чином

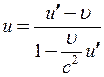, (2)

звідки відносна швидкість частинок 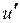буде визначатись так

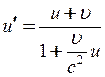. (3)

Зробимо обчислення.

1) .

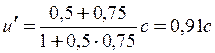2) .

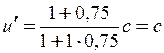Таким чином, 1) ні в одній інерціальній системі відліку швидкість не може бути більшою ніж швидкість світла; 2) швидкість розповсюдження світла у вакуумі абсолютна.

Відповідь: 1). 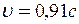; 2) .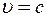

Приклад 15. Визначити релятивістський імпульс електрона, кінетична енергія якого дорівнює 5 МеВ.

Дано: T = 5 МеВ = 8·10^-13 Дж; m = 9,31·10^{-31 кг.}

Знайти: p.

Розв’язок. Імпульс релятивістської частки може бути знайдений з виразу

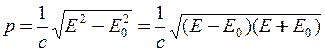, (1)

де Е – повна енергія частинки; Е₀ – енергія спокою частинки, E₀ =mc² = = 0,51 МеВ = 81·10^-13 Дж.

Різниця Е – Е₀ = Т – кінетична енергія частинки; Е + Е₀ = 2Е₀ + Т, (тому що Е = Е₀ + Т). Це дозволяє пов’язати релятивістський імпульс з кінетичною енергією

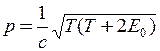. (2)

Тут c – швидкість світла у вакуумі.