Многослойная схема с обратным распространением ошибки

С применением алгоритма Nevada Quickrop на мэйнфрейм-машине Convex были опробованы сети различной архитектуры. Базовая структура сети проста: входной вектор из шести переменных и одномерный выход (переменная VWNY). Остается выбрать число скрытых слоев и число нейронов. Далее, поскольку результаты Чена, Ролла и Росса указывают на присутствие линейных связей между входами и выходом, способность сети к обобщению может быть увеличена за счет прямых связей между входными и выходным элементами. В отсутствие каких-либо готовых схем для оптимального выбора модели исследователь должен опробовать различные статистические критерии согласия. Так, оценивали риск предсказания, полученный при различных архитектурах сети и находили общее число дублирующих друг друга элементов в скрытом слое. Сравнивали величины квадратного корня из среднеквадратичной ошибки (RMSE) на тестовом множестве, состоящем из 60 наблюдений, относящихся к последним 5 годам интервала наблюдений (1981-85 гг.). Для дальнейшей работы была взята та архитектура сети, которая давала наименьшее RМSЕ.

Таблица 4.3

Квадратный корень из средней квадратичной ошибки на подтверждающем множестве для полностью обученных сетей различной архитектуры

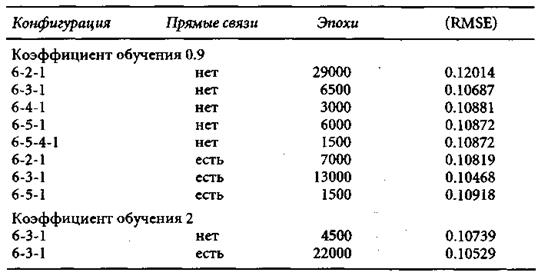
Для того чтобы ошибочно не принять раньше времени локальный минимум погрешности обобщения за глобальный, наш алгоритм брал вдвое большее число эпох по сравнению с тем, на котором достигалось наилучшее обобщение. Таким образом, на самом деле, число эпох было вдвое больше, чем показано в табл. 4.3 и на рис. 4.1. При любом выборе коэффициента обучения ошибка КМ5Е на тестовом множестве оказывалась меньше, чем на обучающем. Этот в некоторой степени удивительный эффект может объясняться наличием белого шума в обучающем множестве и его отсутствием в тестовом множестве. Поскольку обучение прекращалось, как только RMSE на тестовом множестве начинала расти, мы полагаем, что переобучение не имело места, и что сеть не запоминала шум. Таким образом, относительно большая погрешность на обучающем множестве объясняется именно белым шумом.

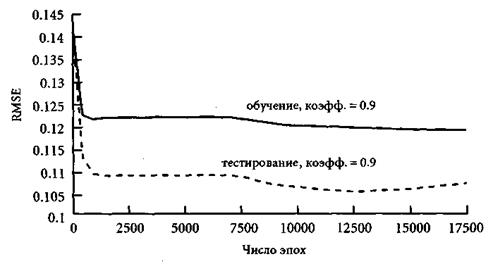
Рис. 4.1. Квадратный корень из среднеквадратичной ошибки для 6-3-1 сети с прямыми связями и коэффициентом обучения 0.9

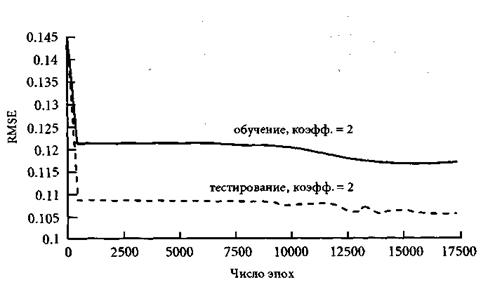
Рис. 4.2. Квадратный корень из среднеквадратичной ошибки для 6-3-1 сети с прямыми связями и коэффициентом обучения 2

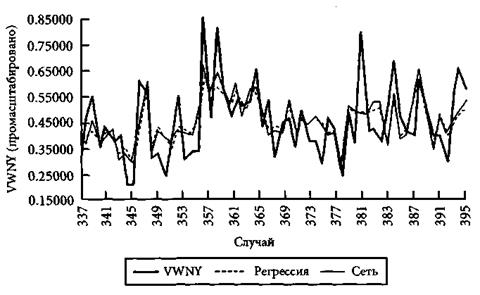
Рис. 4.3. Сравнение оценочных значений переменной VWNY, полученных регрессией и сетью, с ее истинными значениями

Среди всех конфигураций наилучшей (имеющей наименьшее RМSЕ на подтверждающем множестве) оказалась 6-3-1 сеть с прямыми связями и коэффициентом обучения 0.9. Желая получить решение за кратчайшее время (в пределах 13 тыс. эпох), был увеличен коэффициент обучения в два раза (до 2). Шаги в направлении градиента теперь стали очень большими, и мы перескакивали через решение. Поэтому даже оптимально обученной сети понадобилось гораздо больше, чем 13 тыс. эпох (а именно, 22 тыс.). На рис. 4.1 видно, как RMSE быстро убывает в первые 500 эпох, а после 12 тыс. эпох начинает ассоциировать.

Оценки, которые выдала (рис. 4.3), полученные на подтверждающем множестве (которое соответствует 1981-85 гг.) сеть, оказались лучше всех, которые дает регрессионный анализ, как по показателю RMSE, так и коэффициентам корреляции Пирсона. При этом результаты, которые сеть показывает на новых образцах, даже превосходят те, которые регрессия имела на обучающем множестве (REG1).

До сих пор мы сравнивали между собой сетевые архитектуры с различным числом скрытых слоев и нейронов, предполагая, что каждый входной сигнал, действительно, влияет на результат. Однако, как уже говорилось, непредвиденная инфляция (UI) и месячное производство (МР) существенно не влияют на среднеквадратичную ошибку. В связи с этим возникает вопрос о том, нельзя ли эти переменные безболезненно изъять из дальнейшего рассмотрения. Явля-ются ли эти переменные просто несущественными, т.е. не влияющими на выходной сигнал, или же они избыточные, т.е. могут быть представлены в виде линейной (или нелинейной) комбинации остальных?

Таблица 4.4

Критерии согласия для выходов регрессии и сети

Таблица 4.5

. Вклад всех переменных в решение на обучающем, тестовом множествах и на всех данных

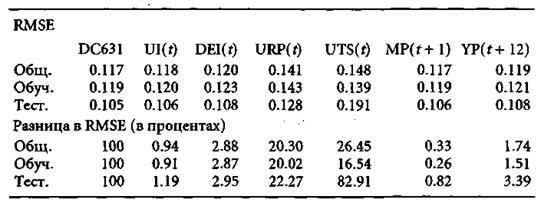
Для оценки вклада переменных вычислялся выход сети с оптимальным вектором весов с помощью пакета Microsoft. Ехсеl. Затем про каждую переменную по очереди временно полагалось, что ее значение неизвестно и должно быть заменено на среднее арифметическое (безусловное ожидание) этих значений при постоянных исходных значениях остальных пяти переменных. В результате получилось 6 новых входных матриц. Затем вычислялись выходы сети для всех этих матриц. Для шести полученных выходных рядов подсчитывалась RMSE и сравнивалась с RMSE исходной входной матрицы. Идея была в том, что для переменной, которая активно влияет на решение, RMSE на соответствующем выходном векторе должна быть заметно больше, чем для исходной входной матрицы.

Все вычисленные таким образом RMSE оказались больше исходной. Такое увеличение означает, что замена переменной ее безусловным ожиданием ухудшает оценку целевой переменной. В случаях с временной структурой и премией за риск рост RMSE был самым большим (соответственно, 83% и 22% на проверочном множестве). Вспомните, что эти две переменные по результатам регрессионного анализа на всех под интервалах также были оценены как имеющие сильное влияние. Далее, выявилось такое любопытное обстоятельство: переменные, которые по результатам регрессионного анализа были квалифицированы как неактивные, на самом деле, влияют на решение. Непредвиденная инфляция и месячная продукция имеют определенную «объясняющую роль» и не могут быть заменены комбинациями других входных переменных.

Различия между сетью и OLS-регрессией становятся разительными, когда в данных присутствуют нелинейности, которые можно уловить с помощью сигмоидальной функции преобразования. Ви-генд ввел следующую меру улучшения результата за счет функции активации по сравнению с OLS:

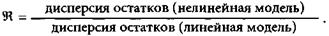
Ее значение всегда лежит в интервале от 0 до 1, поскольку от того, что сеть при обучении улавливает содержащиеся в данных нелинейности, погрешность может только уменьшиться. Значения этого отношения для обучающего и проверочного множеств оказались равны, соответственно, 0.94 и 0.92, и это говорит о том, что либо сеть плохо использует свои нелинейные возможности, либо нелинейностей в данных просто нет. Вероятнее второе, потому что база данных строилась с помощью линейных моделей, для того чтобы выделить взаимно не коррелирующие экономические факторы. Большим значением данного отношения объясняется то обстоятельство, что обученная сеть лишь незначительно превосходит OLS-регрессию по критерию RMSE. Однако остается фактом то, что нейронные сети превосходят OLS-регрессию даже при работе с такими данными, в которых нелинейные связи между входами и целевой переменной выражены слабо.