Простейшие разностные аппроксимации задачи Коши.
Cнова рассматриваем задачу Коши для ОДУ в её обычной постановке:
y¢(x) = f (x, y(x)), xÎ [x0, b] (1)
y (x0) = y 0 (2)
Полагая в выражении (1), что x = xi получим:
y¢ (xi) = f (xi, y(xi) ) (44)
Далее к левой части равенства (44) будем применять приведённые в таблице 2 простейшие аппроксимации производной y¢(x) первого и второго порядков точности.
Таблица 2 -формулы аппроксимации первой производной.
формула левой аппроксимации производной y¢(x) в узле xi:
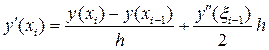 , x i-1 Î(x i-1; xi), , x i-1 Î(x i-1; xi),
|
формула правой аппроксимации производной y¢(x) в узле xi:
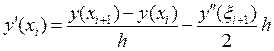 , x i+1 Î(x i; xi+1) , x i+1 Î(x i; xi+1)
|
формула симметричной аппроксимации производной y¢(x) в узле xi:
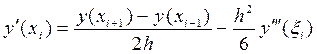 , x iÎ( x i-1; x i+1) , x iÎ( x i-1; x i+1)
|
формулы несимметричной аппроксимации производной y¢(x) второго порядка точности в узле xi:
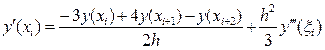 , xiÎ(x i, x i+2), , xiÎ(x i, x i+2),
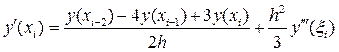 , xiÎ(x i-2, x i). , xiÎ(x i-2, x i).
|
Используя соотношения из таблицы 2 для аппроксимации производной y¢(x) из ОДУ (1), получим следующие выражения для приближённых (явных и неявных) разностных методов решения задачи Коши для ОДУ первого порядка.
y¢(xi) = 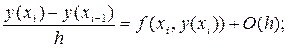 или
или
y¢(xi+1) = 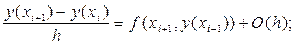 (45)
(45)
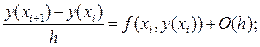 (46)
(46)
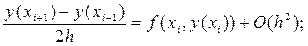 (47)
(47)
 или
или
переписывая это соотношение применительно к узлу (xi-1) получим:
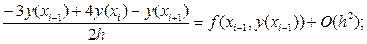 (48)
(48)
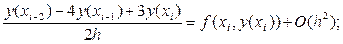 или
или
переписывая это соотношение применительно к узлу (xi+1) получим:
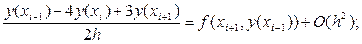 (49)
(49)
Отбрасывая в выражениях (45) - (49) слагаемое, характеризующее порядок аппроксимации производной и заменяя в них точные значения y (xj) решения y (x)
в j-х узлах сетки wh = { x i|x i = x0 + ih (i = 0,1, …, n) } приближёнными значениями
yj получаем следующую совокупность разностных схем решения задачи Коши:
Из (45) Þ yi+1 = yi + h f (xi , yi) (i = 0,1, …, n - 1); (50)
Из (46) Þ yi+1 = yi + h f (xi+1, yi+1) (i = 0,1, …, n - 1); (51)
Из (47) Þ yi+1 = yi-1 + 2h f (xi, yi) (i = 1,2…, n - 1); (52)
Из (48) Þ yi+1 = 4yi -3yi-1 - 2h f (xi-1 , yi-1) (i = 1,2…, n - 1); (53)
Из (49) Þ yi+1 = 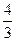 yi -
yi - 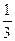 yi-1 +
yi-1 + 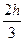 f (xi+1, yi+1) (i = 1,2…, n - 1). (54)
f (xi+1, yi+1) (i = 1,2…, n - 1). (54)
Первые две схемы (50) и (51) являются явной и неявной схемой Эйлера, которые рассмотрены раньше, остальные методы (52) – (54) являются двухшаговыми.
Дата добавления: 2015-09-14; просмотров: 1712;
