Методы Рунге-Кутта четвёртого порядка.
Наиболее употребительными на практике являются методы Рунге-Кутта четвёртого порядка, на каждом шаге вычисления численная схема определяется следующей последовательностью выражений:
Пусть с i - го шага известно приближённое значение yi решения y(xi) задачи Коши в узле xi, тогда приближённое значение yi+1 решения y(xi+1) на следующем шаге (т.е. в следующем узле xi+1 сетки) находится по схеме:
y(xi+1) » 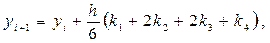 где: где:
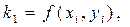
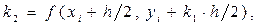
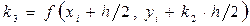 , ,
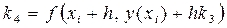 . .
| (36) |
Обоснование формул метода Рунге-Кутта четвёртого порядка [4, стр. 158], основанное на интегрировании исходного ОДУ и использовании для интегрирования формулы Симпсона, приведено ниже в приложении к данной лекции.
Схемы Рунге-Кутта обладают важными достоинствами: все они имеют хорошую точность; они являются явными; допускают расчёт с переменным шагом; легко обобщаются на случай систем дифференциальных уравнений. Именно благодаря этим свойствам методы Рунге-Кутта часто используются при решении задач Коши на ЭВМ.
Рекомендации.
Если правая часть дифференциального уравнения (1) ограничена вместе со своими производными до четвёртого порядка, то схема (36) даёт хорошие результаты благодаря малому коэффициенту в остаточном члене и быстрому возрастанию точности схемы при уменьшении шага. Если же указанных производных у правой части нет, то не худшую точность имеют схемы и меньшего порядка, например, схема (30).
Дата добавления: 2015-09-14; просмотров: 1220;
