Семейство методов Рунге-Кутта.

Исправленный метод Эйлера (13) и другие методы, основанные на пошаговом представлении решения y(x) задачи Коши (1),(2) рядом Тейлора, требуют последовательного дифференцирования уравнения (1) для получения тейлоровских коэффициентов (которыми являются производные различных порядков от решения y(x)). Это приводит к необходимости вычисления на каждом шаге частных производных от неявной функции f (x, y). Это является одним из недостатков таких методов.

В этой связи привлекательной является идея построения методов Рунге-Кутта, которые хотя и основаны на разложении искомого решения y(x) в ряд Тейлора, но не требуют вычисления частных производных неявной функции f (x, y).

Пусть известно разложение по формуле Тейлора для искомого решения y(x_i+1) в окрестности точки x_i:

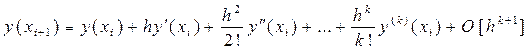(14)

Перепишем это выражение в виде:

(15)

Полином 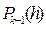в правой части формулы (15) представляет собой фрагмент исходного ряда Тейлора (14), содержащий значения производных y¢(x_i), y¢¢(x_i),…, y^(k)(x_i) искомого решения в точке x_i.

Идея Рунге метода Рунге – Кутта [2, стр.116] состоит в том, чтобы, используя метод неопределённых коэффициентов, аппроксимировать (с тем же порядком точности 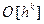) данный полином:

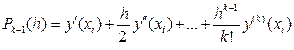(16)

некоторой функцией j (x, y, h), не содержащей частных производных от функции
f (x, y). В результате чего формулу (15) можно будет переписать в виде:

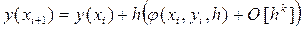
(17)

Метод Рунге-Кутта первого порядка.

Если искомое решение y(x_i+1) представить рядом Тейлора первого порядка по h т.е. с точностью до слагаемых линейных по h:

,

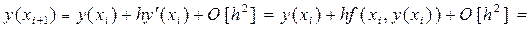
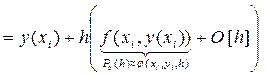то в соответствии с идеей метода Рунге-Кутта в качестве функции j (x_i, y_i, h), аппроксимирующей с порядком точности 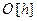фрагмент ряда Тейлора 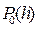следует выбрать функцию j (x_i, y_i, h) = f (x_i, y_i).

Таким образом, при представлении решения y(x_i+1) рядом Тейлора первого порядка (случай k = 1) определяющее метод Рунге-Кутта выражение (17) превращается в формулу Эйлера:

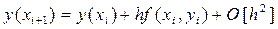
И, следовательно, можно считать, что метод Эйлера является простейшим примером метода Рунге-Кутта первого порядка.

Метод Рунге-Кутта второго порядка.

Метод Рунге-Кутта второго порядка соответствует случаю, когда искомое решение y(x_i+1) представляется рядом Тейлора с точностью до слагаемых второго порядка по h:

(18)

В этом случае соотношение (17), определяющее метод Рунге-Кутта, имеет вид:

(19)

Поэтому в соответствии с идеей метода Рунге-Кутта параметры функции j(x, y, h) подбирают, из условия, что она должна аппроксимировать с точностью до слагаемых линейных по h полином:

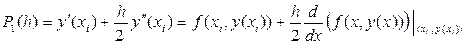(20)

Для того, чтобы определить вид функции j(x, y, h), аппроксимирующей полином (20), перепишем аппроксимируемый полином в несколько ином виде.

Если для аппроксимации производной 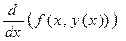, входящей в правую часть выражения (20) использовать разностное отношение общего вида:

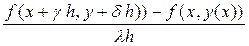
где l, g и d - некоторые пока неизвестные параметры, то аппроксимируемый полином (20) можно переписать в виде:

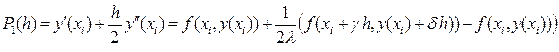(21)

Отсюда ясно, что функцию j (x_i, y_i, h) аппроксимирующую полином (21) можно взять в виде выражения:

j (x_i,y_i, h) = b f (x_i, y(x_i)) + a f (x_i +g h, y(x_i) + d h). (22)

Здесь b, a, g и d - неизвестные параметры, значения которых нужно определить.

В результате с учётом вида функции j (x_i,y_i, h), определяемой выражением (22), формула (18), определяющая метод Рунге-Кутта второго порядка, может быть переписана в виде:

y(x_i+1) = y(x_i) + h×( b f (x_i, y(x_i)) + a f (x_i +g h, y(x_i) + d h) + 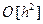) (23)

Поскольку функция j (x_i,y_i, h) (22) должна аппроксимировать полином (20), содержащий линейные слагаемые по h, то функцию f ( x_i +g h, y(x_i) + d h ) из выражения (22) раскладывают в ряд Тейлора с точностью до линейных по h слагаемых:

f (x_i +g h, y(x_i) + d h) = f (x_i, y(x_i) ) +g h f¢_x(x,y(x)) 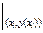+ d h f¢_y(x,y(x)) + 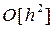(24)*

(* Схема разложения функции двух переменных в ряд Тейлора [3, стр. 266] приведена для справок в приложении к данной лекции).

Подставляя разложение (24) в формулу (23) получим следующую формулу для выражения метода Рунге-Кутта второго порядка:

y(x_i+1) = y(x_i) + h(b +a) f (x_i, y(x_i)) + a h²(g f¢_x(x, y(x)) + d f¢_y(x, y(x)) 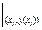) + (25)

Далее неизвестные параметры b, a, g и d,в формуле (25), определяют так, чтобы представляемое формулой (25) разложение решения y(x_i+1) с тем же порядком 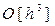аппроксимировало разложение (18) решения y(x_i+1) в ряд Тейлора:

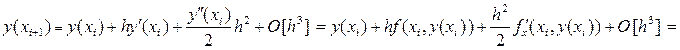
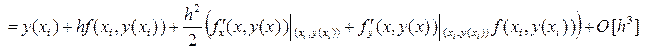(26)

Приравнивая в формулах (25) и (26) коэффициенты в главных порядках по h найдём, что параметры b, a, g и d, определяющие функцию j (x_i,y_i, h) (22) должны удовлетворять следующей совокупности условий:

(b + a) = 1; a g = 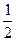; a d = 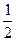f (x_i, y(x_i)); Û 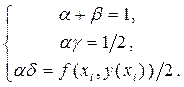(27)

Полученная система уравнений (27) содержит три уравнения относительно четырёх параметров b, a, g и d. Это свидетельствует о наличии одного свободного параметра, через который можно выразить остальные параметры.

Выражая из (27) параметры b, g и d через параметр a получим:

b = 1 - a, g = 1/2 a и d = 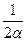f (x_i, y(x_i)) (28)

В результате подстановки этих значений параметров в формулу (23) приходим к однопараметрическому семейству методов Рунге - Кутта второго порядка.

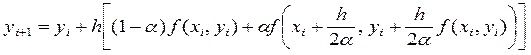(29)

где a (0 < a £ 1) является параметром семейства методов решения задачи Коши.

Схема реализации методов Рунге-Кутта второго порядка.

При реализации вычислительного процесса на ЭВМ любой метод из семейства методов Рунге-Кутта второго порядка (29) реализуют по следующей схеме.

1. На каждом шаге, т.е. при каждом i = 0,1, 2, … , вычисляют значения функций: h i1 = f (xi, y(xi)), h i2 = 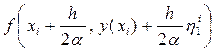. 2. Затем находят шаговую поправку Dy(xi) = h[(1 - a)h i1 + a)h i2], прибавление которой к результату предыдущего шага даёт приближённое значение решения y (x) в точке xi+1 = xi + h: y(xi+1) = y(xi) + Dyi. Методы такой структуры называют двухэтапным по количеству вычислений значений функции (т.е. правой части дифференциального уравнения (1)) на одном шаге.

(30)

Частные случаи методов Рунге-Кутта второго порядка.

Выделим из семейства методов (29) два наиболее простых частных случая, соответствующих значениям a = 1 и a = 1/2.

1.)При a = 1 семейство методов Рунге-Кутта (29) приобретает наиболее простой вид, который называется методом средней точки:

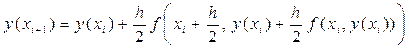(31)

Поясним на рис. 1 графически смысл метода средней точки.

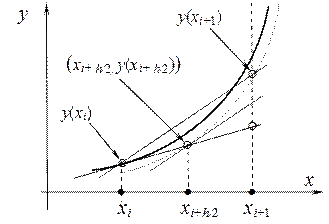
Рисунок 1 – Геометрическая иллюстрация метода Рунге-Кутта второго порядка

Сначала через точку x_i проводим касательную, наклон которой определяем из исходного уравнения:

y(x)= y(x_i) + f (x_i, y(x_i))(x - x_i) (32)

Далее делаем половинный шаг по схеме ломанных, т.е. находим значение данной касательной (32) в точке x_i+h/2:

y(x_i+h/2)= y(x_i) + 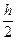f (x_i, y(x_i)) (33)

Затем из дифференциального уравнения (1) определяем наклон интегральной кривой y¢(x) в данной точке (x_i+h/2, y(x_i+h/2)), т.е. находим чему был бы равен наклон интегральной кривой y¢(x), если бы она проходила через точку (x_i+h/2, y(x_i+h/2)):

y¢(x_i+h/2) = f (x_i+h/2, y(x_i) + 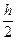f (x_i, y(x_i)) ) (34)

По этому наклону (34) и определяем окончательно приращение искомого решения y(x_i) на целом шаге h:

y(x_i+1) - y(x_i) = h y¢(x_i+h/2) = h f (x_i+h/2, y(x_i) + 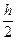f (x_i, y(x_i)) ) (35)

2.)При a = 1/2 формула (29) превращается в рассмотренный ранее метод Хьюна:

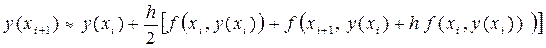, (i = 0,1, …, n),

Замечания.

1. Выбрать параметр a так чтобы схема (29) давала бы аппроксимацию третьего порядка невозможно.

2. Приведём без доказательства теорему о сходимости и точности методов Рунге-Кутта второго порядка.

Теорема. Если функция f (x, y(x)) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по схеме (29), равномерно сходится к точному решению с погрешностью 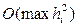, т.е. данный метод Рунге-Кутта имеет второй порядок точности.