Оценка глобальных ошибок вычислительных процессов решения начальной задачи для ОДУ.

До сих пор используемые вычислительные методы характеризовались только локальными (одношаговыми) ошибками, возникающими при реализации метода на одном текущем шаге вычислительного процесса в предположении, что исходным материалом для получения результата этого шага служат точные значения.

Для оценки качества используемых численных методов необходимо также описать поведение ошибок в их взаимосвязи на соседних шагах и изучить процесс накопления методической погрешности вычислительного метода к n-му шагу его реализации.

Знание того, как изменяются погрешности от шага к шагу, позволяет делать выводы о численной устойчивости разностного метода и о сходимости поставляемых им каркасов приближённых решений, а также получать оценки глобальной погрешности численного метода. Приведём определения используемых понятий устойчивости метода и сходимости каркасов решений.

Определение 1. Вычислительный процесс (метод) называется устойчивым, если малые погрешности исходных данных вызывают малые погрешности вычисляемого результата (т.е. если рост погрешности в процессе вычисления ограничен).

Обозначим через y(x)_h значения функции y(x) – точного решения задачи Коши (3), (4) на сетке w_h = {x _i|x _i = x₀ + ih (i = 0,1, …, n)}, т.е. y(x)_h это значения функции точного решения y(x) в узлах сетки w_h. Предположим так же, что y(x) – непрерывная функция.

Рассмотрим погрешность Z_h = u(x)_h - y(x)_h, где u(x)_h – каркас решения данной задачи Коши на сетке w_h, полученный с использованием некоторой разностной схемы или численного метода.

Определение 2. Говорят, что имеет место сходимость разностной схемы (или некоторого пошагового приближённого метода), используемой для получения каркаса приближённого решения u(x)_h к соответствующему точному решению y(x)_h задачи Коши (3) - (4), если 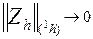при |h| ® 0. Говоря иначе, разностная схема сходится, если последовательность величин Z_h = u(x)_h - y(x)_h, при |h| ® 0 сходится к нулю по норме или равномерно, как величина первого порядка малости по h.

На практике изучение вопросов сходимости каркасов, поставляемых приближёнными методами решения задачи Коши, позволяет ответить на вопрос, можно ли приближённым решением u(x)_h сколь угодно хорошо охарактеризовать (т.е. отобразить или смоделировать) поведение точного решения y(x)_h.

Оценка глобальной погрешности метода Эйлера.

Рассматриваем задачу Коши для ОДУ в её обычной постановке (1), (2):

y¢(x) = f (x,y), xÎ [x₀, b] (1)

y (x₀) = y ₀ (2)

Обозначим через d_i разность между значением точного решения y = y(x_i) задачи Коши в i - м узле сетки w_h и соответствующей компонентой каркаса решения (иначе говоря, таблицы полученных приближённых значений решения y = y(x_i)), полученного тем или иным разностным методом.

d_i = y (x_i) - y_i (55)

Предположим, что правая часть ДУ (т.е. функция f (x, y(x) ) и решение y(x) задачи Коши обладают достаточной гладкостью и выполняются условия:

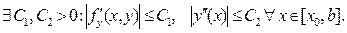(56)

В рамках данных требований проведём оценку глобальной погрешности метода Эйлера, для этого:

1. В окрестности точки x_i запишем разложение точного решения y = y (x) задачи Коши в ряд Тейлора с точностью до линейного слагаемого:

y(x) = y(x_i) + 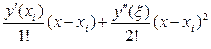, где xÎ(x, x_i).

Отсюда, для значения решения в узле x_i+1 получим:

y(x _i+1) = y(x_i) + 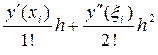, где x_iÎ(x_i, x_i+1). (57)

2. Поскольку для оценки пошаговой погрешности метода Эйлера необходимо рассмотреть величину d_i = y (x_i) - y_i, то вычтем из линеаризованного по формуле Тейлора (57) разложения точного решения y(x_i+1) задачи Коши приближённое решение y_i+1, полученное на основе явного метода Эйлера:

y_i+1 = y_i + h f (x_i, y_i). (58)

3. Вычитая из (57) соотношение (58) и заменяя в полученном выражении y¢(x_i) на f (x_i,y(x_i)), в соответствии с обозначением (55) получим:

d_i+1 = y (x_i+1) - y_i+1 = y(x_i) + 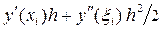- y_i - h f (x_i, y_i) Þ

d_i+1 = d_i + h [f (x_i, y(x_i)) - f (x_i, y_i)] + 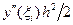(59)

Применив в выражении (59) к разности функций в квадратных скобках формулу
конечных приращений Лагранжа по второму аргументу:

f (x_i, y(x_i)) - f (x_i, y_i) = f¢_y(x_i, q_i) d_i, где d_i = y (x_i) - y_i.

получаем разностное уравнение, связывающее ошибки в (i + 1)-м и i-м узлах:

d_i+1 = d_i + h f¢_y(x_i, q_i) d_i + 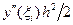^* (60)

здесь x_i и q_i - некоторые точки из области задания и области значения решения y(x) соответственно.

(*сведения о формуле конечных приращений Лагранжа приведены в приложении к данной лекции [3, стр. 180]).

Для дальнейшего анализа выражение (60) целесообразно переписать в более компактном виде (62) с использованием следующих обозначений:

А_i = 1+ h f¢_y(x_i, q_i), В_i = 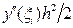(61)

d_i+1 = А_id_i + В_i, (i = 0,1, …, n - 1); (62)

Поскольку в соответствии с (55) d_i+1 = y (x_i+1) - y_i+1 и d_i = y (x_i) - y_i то, используя соотношение (62), проведём оценивание абсолютной погрешности получаемых приближённых значений y_i+1, y_i решения задачи Коши:

d_i+1 £ |А_id_i| + |В_i| (63)

Поскольку А_i = 1 + h f¢_y(x_i, q_i), В_i = 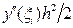, то из (63), используя ограничения, накладываемые на функции f (x, y) и y(x) условиями

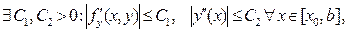
можем написать рекуррентное неравенство:

|d_i+1| £ А|d_i| + В, (i = 0,1, …, n - 1); (64)

где

А = 1 + С₁h, В = 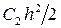. (65)

Итерирование неравенства (64) даёт:

|d_i+1| £ А(А|d_i-1| + В) + В = А²|d_i-1| + (А+1)В) £

£ А²(А|d_i-2| + В) + (А+1)В) = А³|d_i-2| + (А²+А+1)В) £ …

и поскольку согласно начальному условию d₀ = y (x₀) - y₀ = 0, то последнее неравенство можно переписать в виде:

… £ Аⁱ⁺¹ |d₀| + (Аⁱ+ А^i-1 +…+ A + 1) В = .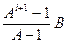

Отсюда окончательно имеем:

|d_i+1| £ 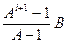(66)

Сумма Аⁱ+ А^i-1 +…+ A + 1 = 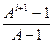в выражении (66) вычислена по формуле суммы n -первых членов геометрической прогрессии: 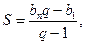где в данном случае
n = i, b₁ = 1, b_n = Аⁱ, q = A.

При i = n- 1 в соответствии с обозначением для А и В (65) из соотношения (66) получаем оценку для глобальной погрешности метода Эйлера:

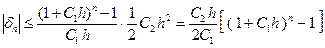(67)

Чтобы разобраться с полученным выражением (67) для глобальной погрешности и оценить его порядок, применим к правой части выражения (67) формулу бинома Ньютона n - й степени:

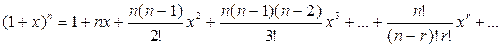
В соответствии с данной формулой бинома Ньютона .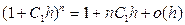

Учитывая, что 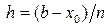, в результате из (67) получаем:

|d_n| = |y(b) - y_n| 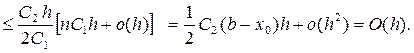(68)

Глобальная погрешность метода Эйлера имеет первый порядок относительно шага h и совпадает по порядку с погрешностью аппроксимации дифференциальной начальной задачи (1) – (2) дискретной задачей (50): y_i+1= y_i + h f (x_i , y_i)
с начальным значением y₀.

Заключение (план - аннотация лекции №23).

В лекции 23 изучаются приближённые методы решения задачи Коши, основанные на применении формулы Тейлора. Рассмотрен исправленный метод Эйлера, основанный разложении точного решения y(x) задачи Коши в ряд Тейлора и последовательном дифференцировании исходного ДУ для получения коэффициентов Тейлоровского разложения.

Обсуждается идея построения методов Рунге-Кутта, которые хотя и основаны на разложении искомого решения y(x) в ряд Тейлора, но не требуют вычисления частных производных неявной функции f (x, y). Дан вывод методов Рунге-Кутта первого и второго порядка, рассмотрена геометрическая интерпретация метода Рунге-Кутта второго порядка. Приведены формулы метода Рунге-Кутта четвёртого порядка, вывод которых дан в приложении к данной лекции. Даны рекомендации по использованию методов Рунге-Кутта, охарактеризованы свойства сходимости и точности методов Рунге-Кутта.

Рассмотрено применение метода Рунге-Кутта четвёртого порядка для численного решения нормальных систем.

Рассмотрен разностный способ решения задачи Коши, который основан на замене (т.е. на аппроксимации) входящей в ДУ производной y¢(x) каким-либо разностным отношением, т.е. на использовании формул аппроксимаций производной, рассмотренных при изучении численного дифференцирования. Приведены примеры простейших разностных аппроксимаций задачи Коши.

Дано понятие шаговой, т.е. локальной ошибки приближённого метода решения задачи Коши, допускаемой на каждом шаге метода решения. Рассмотрены подходы к оценкеглобальных ошибок вычислительных процессов решения задачи Коши для ОДУ, для этого даны определения понятий устойчивости приближённых методов решения задачи Коши и сходимости полученных на его основе каркасов решений. Получена формула для оценки глобальной погрешности метода Эйлера.

Приведены примеры решения типовых задач.

Литература:

1. В.М. Вержбицкий. Основы численных методов. – М.: Высшая школа, 2002. – 840 стр.

2. Приклонский В.И. Численные методы. Лекционный курс, читаемый в МГУ. Адрес в Интернете ttp://afrodita.phys.msu.ru/download/priklonsky/lections/

3. Г.М. Фихтенгольц. Основы математического анализа, том 1. – М.: Наука, 1968. – 440 с.

4. В.Ф. Формалёв, Д.Л. Ревизников. Численные методы. – М.: Физматлит, 2004. 400 с.