Приложение. 1. Ряд Тейлора для функции двух переменныхf (x, y).
1. Ряд Тейлора для функции двух переменныхf (x, y).
Рассмотрим функцию двух переменных f (x, y), тогда если x и y принадлежат некоторой окрестности точки (a, b), то функцию f (x, y) в окрестности точки (a, b) можно представить в виде ряда Тейлора, т.е. в виде разложения по степеням разностей (x - a) и (y - b):
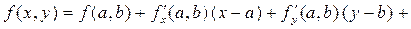 O{max[(x - a)2, (y - b)2]}.
O{max[(x - a)2, (y - b)2]}.
Данное разложение представлено с точностью до линейных значений разностей (x - a) и (y - b).
2. Теорема о конечных приращениях Лагранжа.
Теорема Лагранжа(для случая функции одной переменной).
Пусть:
1. Функция f (x) определена и непрерывна в замкнутом промежутке [а, b];
2. Существует конечная производная f¢ (x), по крайней мере, в открытом промежутке (а, b).
Тогда: между а и b найдётся такая точка с (а < с < b), что для неё выполняется неравенство:
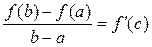 или
или 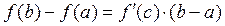
Данное соотношение называется формулой Лагранжа или формулой конечных приращений.
Если вместо f (x) рассматривается функция двух переменных f (x, y), удовлетворяющая требованиям теоремы Лагранжа по второму аргументу - y, то на основе теоремы Лагранжа можем написать: 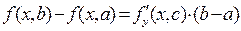 .
.
Дата добавления: 2015-09-14; просмотров: 1133;
