Приложение. 1. Скалярное произведение функций.

1. Скалярное произведение функций.

Пусть на отрезке [a, b] задана система функций, интегрируемых с квадратом на [a, b]:

u₀(x), u₁(x), u₂(x), …, u_n(x), …, (1)

Аналогично тому, как между элементами векторного пространства вводится операция скалярного произведения векторов, которая сопоставляет паре векторов данного пространства некоторое число – скаляр, так и между элементами данной системы функций u_i(x), u_j(x) может быть определена операция скалярного произведения функций, обозначаемая далее как (u_i (x), u_j (x) ).

По определению операция скалярного произведения между элементами x, y и z некоторого пространства (в том числе и между элементами системы функций) должна обладать следующими свойствами:

Скалярное произведение между элементами пространства функций u_i(x), u_j(x) i, j = 0, 1, 2,..., интегрируемых на [a, b] с квадратом, вводится с помощью операции интегрирования:

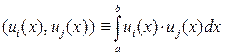(3)

Определение 1. Система (1) является ортогональной системой функций на отрезке [a, b], если любые две функции u_i(x), u_j(x), i, j = 0, 1, 2, ... данной системы
ортогональны (между собой) на [a, b].

Определение 2. Назовём две функции u_i (x), u_j (x), i, j = 0, 1, 2, ... системы (1)
ортогональными на отрезке [a, b], если для их скалярного произведения выполняется условие:

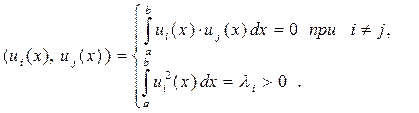(4)

Число 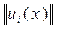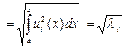- называется нормой функции u_i (x).

Если все функции u_i (x) имеют единичную норму, т.е.

l_i = 1, i = 0, 1, 2, ... (5)

и система функций (1) ортогональна на [a, b], то такая система называется
ортонормированной или нормальной ортогональной системой на отрезке [a, b].

Если условия нормальности функций изначально не выполняются, от системы (1) при необходимости можно перейти к системе (6), которая уже заведомо будет нормальной:

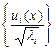, i = 0, 1, 2, ... (6)

Отметим, что из свойства ортогональности элементов некоторой системы, следует их линейная независимость, т.е. справедливо утверждение: Всякая ортогональная система ненулевых векторов (элементов) является линейно-независимой.

2.Понятие базисных функций.

Из курса линейной алгебры вам известно, что в пространстве векторов можно ввести векторный ба́зис - множество векторов, таких, что любой вектор данного векторного пространства может быть единственным образом представлен в виде линейной комбинации базисных векторов. При этом ни один из базисных векторовне представим в виде конечной линейной комбинации остальных базисных векторов (линейная независимость базисных векторов).

Так, например, любой вектор 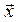трёхмерного пространства однозначно может быть представлен в виде линейной комбинации базисных векторов :

= .

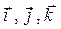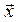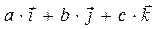где a, b, и c - некоторые числа. А в силу линейной независимости (ортогональности) базисных векторов 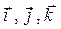ни один из векторов 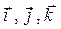в отдельности не может быть представлен в виде линейной комбинации оставшихся базисных векторов.

Аналогично изложенному выше, в пространстве полиномиальных функций, т.е. в пространстве полиномов степени не выше n:

P_n(x) = a₀ + a₁ x + a₂ x² + … + a_n xⁿ. (7)

может быть введён базис из элементарных полиномиальных (показательных) функций:

x⁰, x, x², x³, …, xⁿ (8)

при этом, очевидно, что базисные функции (8) являются линейно независимыми, т.е. ни одна из базисных функций (8) не может быть представлена в виде линейной комбинации оставшихся базисных функций. При этом очевидно, что любой полином степени не выше n может быть однозначно представлен в виде (7), т.е. в виде линейной комбинации базисных функций (8).

Далее, не углубляясь в теорию, отметим, что многие дифференцируемые функции могут быть представлены в виде линейных комбинаций базисных функций из семейства полиномиальных (показательных) функций вида:

j _i(x) = g_i(x - a) ⁱ + (x - a) ^{i+ 1}, i = 1, 2, …, n (9)

Объяснение этому отчасти даётся известной из математического анализа теоремой Вейерштрасса, в соответствии с которой любая непрерывная на отрезке [a, b] функция f (x) может быть «хорошо» приближена на этом отрезке некоторым полиномом P_n(x) степени n [1, стр. 393], т.е. увеличивая степень n полинома P_n(x), его всегда можно сколь угодно близкоподогнать к непрерывной функции f (x).

Поскольку любой полином может быть представлен в виде линейной комбинации базисных полиномиальных функций типа (8) или (9), то в силу теоремы Вейерштрасса непрерывную (т.е. дважды дифференцируемую функцию, являющуюся решением дифференциального уравнения второго порядка) можно представить в виде линейной комбинации базисных функций (9), которые являются дважды дифференцируемыми и попарно линейно-независимыми.

Вопросы по теме

«Методы приближённого решения краевых задач для обыкновенных
дифференциальных уравнений».

(Лекции 25 - 26)

1. Основные определения: Постановка линейной краевой задачи для ОДУ второго порядка; типы и классификация краевых задач.

2. Методы сведения краевых задач к начальным задачам: постановка задачи; метод пристрелки; метод редукции; метод дифференциальной прогонки.

3. Метод конечных разностей: постановка задачи; универсальность метода конечных разностей для решения краевых задач; выбор типов аппроксимаций производной для сведения краевой задачи к САЛУ с матрицей, имеющей трёхдиагональную структуру.

4. Интерполяционный метод или метод коллокации: поиск приближённого решения в виде линейной комбинации базисных функций, требования к базисным функциям для выполнения краевых условий; поиск коэффициентов линейной комбинации исходя из условия совпадения точного и приближённого решения в узлах коллокации; выбор базисных функций.

5. Метод Галёркина - основные понятия теории метода Галеркина. Поиск приближённого решения в виде линейной комбинации базисных функций, требования к базисным функциям. Выбор коэффициентов линейной комбинации, определяющей вид приближённого решения из условия минимизации невязки, обусловленной заменой точного решения дифференциальной задачи искомым приближённым решением.