Лекция 8. Приложение уравнений Лагранжа 2-го рода к относительному движению
Во многих технически важных задачах механики необходимо исследовать движение механических систем не относительно неподвижной системы отсчета, а по отношению к движущейся с некоторым телом системе координат. Например, движение деталей двигателя внутреннего сгорания удобно рассматривать относительно корпуса двигателя, т.е. относительно транспортного средства, а не относительно дороги. Поэтому имеет смысл поставить задачу вывода уравнений движения механической системы относительно подвижных осей координат, движение которых в неподвижной системе осей задано.
Существует 3 способа формирования уравнений движения МС в этом случае.
Способ 1. На основе кинематики сложного движения точки.Рассмотрим рис. 8.1. Здесь показаны оси подвижной СК Axyz, относительно которых необходимо определить движение заданной механической системы. Показаны также оси неподвижной СК Ooxoyozo, относительно которой задано движение подвижной СК Axyz.
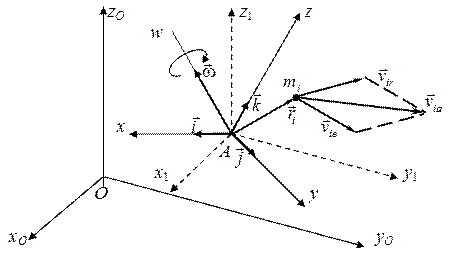
Рис. 8.1. Разложение абсолютной скорости точки системы,
подвижная, неподвижная и вспомогательная системы координат
Для нахождения относительного движения системы по отношению к осям Axyz, совершающим известное движение, достаточно применить уравнения Лагранжа к абсолютному движению, выбирая в качестве параметров переменные 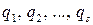 , определяющие положение системы относительно подвижных осей Axyz. Эти же параметры определяют, очевидно, положение системы и относительно неподвижных осей Ooxoyozo, так как движение осей Axyz задано.
, определяющие положение системы относительно подвижных осей Axyz. Эти же параметры определяют, очевидно, положение системы и относительно неподвижных осей Ooxoyozo, так как движение осей Axyz задано.
Абсолютная кинетическая энергия Та системы будет функцией от 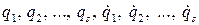 и, быть может, также времени t. С другой стороны, если сообщить системе возможное перемещение, допускаемое связями, имеющими место в момент t, т. е. перемещение, которое получится, если, оставляя t постоянным, сообщить параметрам
и, быть может, также времени t. С другой стороны, если сообщить системе возможное перемещение, допускаемое связями, имеющими место в момент t, т. е. перемещение, которое получится, если, оставляя t постоянным, сообщить параметрам 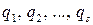 бесконечно малые произвольные приращения
бесконечно малые произвольные приращения 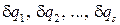 , то сумма работ приложенных активных сил будет выражаться следующим образом:
, то сумма работ приложенных активных сил будет выражаться следующим образом:
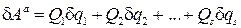 .(8.1)
.(8.1)
Тогда уравнения движения будут
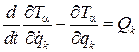 , k=1,2,...,s. (8.2)
, k=1,2,...,s. (8.2)
Если заданные силы имеют силовую функцию U (или потенциальную энергию 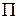 ), то величины Qk будут равны
), то величины Qk будут равны 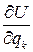
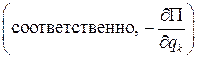 .
.
Для вычисления Ta не обязательно составлять выражения абсолютных координат в функции 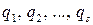 и t. Абсолютная скорость точки mk есть результирующая ее относительной скорости
и t. Абсолютная скорость точки mk есть результирующая ее относительной скорости 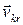 по отношению к движущимся осям Axyz и ее переносной скорости
по отношению к движущимся осям Axyz и ее переносной скорости 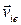 при движении вместе с этими осями. Если обозначить через хi, уi, zi координаты точки mi и точками сверху — производные по времени, то проекции скорости
при движении вместе с этими осями. Если обозначить через хi, уi, zi координаты точки mi и точками сверху — производные по времени, то проекции скорости 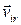 на Axyz будут
на Axyz будут 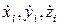 . Что касается переносной скорости
. Что касается переносной скорости 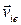 , то это будет скорость, которой обладала бы точка mi, если бы она была связана с осями Axyz. Она является, следовательно, результирующей двух скоростей: поступательной скорости
, то это будет скорость, которой обладала бы точка mi, если бы она была связана с осями Axyz. Она является, следовательно, результирующей двух скоростей: поступательной скорости 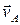 , равной и параллельной скорости точки A, и скорости, вызванной вращением с угловой скоростью w вокруг некоторой оси, проходящей через точку A (оси Aw на рис. 8.1). Обозначая через
, равной и параллельной скорости точки A, и скорости, вызванной вращением с угловой скоростью w вокруг некоторой оси, проходящей через точку A (оси Aw на рис. 8.1). Обозначая через 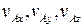 проекции скорости
проекции скорости 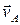 и через р, q, r — проекции угловой скорости
и через р, q, r — проекции угловой скорости 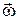 на подвижные оси, мы получим для проекций переносной скорости
на подвижные оси, мы получим для проекций переносной скорости 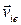 на те же оси выражения
на те же оси выражения 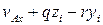 , ... . Следовательно, проекции абсолютной скорости
, ... . Следовательно, проекции абсолютной скорости 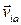 точки mi на подвижные оси Axyz равны
точки mi на подвижные оси Axyz равны 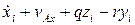 и мы имеем:
и мы имеем:
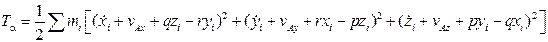 . (8.3)
. (8.3)
Это выражение позволяет вычислить Ta в функции 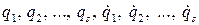 и t, так как координаты хi, уi, zi различных точек суть функции параметров
и t, так как координаты хi, уi, zi различных точек суть функции параметров 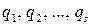 и, быть может, времени t, a
и, быть может, времени t, a 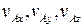 , p, q, r являются известными функциями времени.
, p, q, r являются известными функциями времени.
Способ 2. На основе принципа д’Аламбера. Допустим, что требуется найти движение системы, по отношению к осям Axyz, перемещающимся известным нам образом. Положение системы относительно этих осей зависит от некоторого числа геометрически независимых параметров 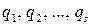 . С другой стороны, система находится под действием заданных сил, и если, дав параметрам приращения
. С другой стороны, система находится под действием заданных сил, и если, дав параметрам приращения 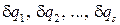 сообщить системе возможное перемещение, допускаемое связями, то сумма элементарных работ этих сил будет иметь вид (8.1).
сообщить системе возможное перемещение, допускаемое связями, то сумма элементарных работ этих сил будет иметь вид (8.1).
Мы можем рассматривать движущиеся оси как неподвижные при условии присоединения к силам, действительно действующим на каждую точку массы mi переносных и кориолисовых сил инерции. Пусть
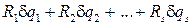 (8.4)
(8.4)
— сумма виртуальных работ этих фиктивных сил на перемещении 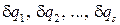 . Тогда можно будет применить уравнения Лагранжа к движению системы относительно осей Axyz, рассматриваемых как неподвижные. Для этого нужно будет составить выражение Tr кинетической энергии системы в ее движении относительно этих осей; это выражение будет функцией обобщенных координат и обобщенных скоростей
. Тогда можно будет применить уравнения Лагранжа к движению системы относительно осей Axyz, рассматриваемых как неподвижные. Для этого нужно будет составить выражение Tr кинетической энергии системы в ее движении относительно этих осей; это выражение будет функцией обобщенных координат и обобщенных скоростей 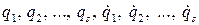 и, быть может, времени t; уравнения движения будут
и, быть может, времени t; уравнения движения будут
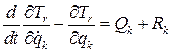 , k=1,2,...,s. (8.5)
, k=1,2,...,s. (8.5)
Способ 3. Смешанный метод Жильбера. Опираясь частично на теорию относительного движения, Жильбер использовал следующий метод. (Gilbert Philippe, Application de la methode de Lagrange a divers problemes de mouvement relatif, Annales de la Societe scientifique de Bruxelles, 1883.)
Пусть, как и раньше, требуется найти движение системы относительно осей Axyz, совершающих известное движение. Предполагается, что положение системы относительно этих осей зависит от s геометрически независимых параметров 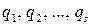 и сумма виртуальных работ приложенных сил на перемещении
и сумма виртуальных работ приложенных сил на перемещении 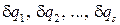 определится по формуле (8.1)
определится по формуле (8.1)
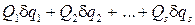 .
.
Проведем через подвижное начало A вспомогательные оси Ax1y1z1, параллельные неподвижным осям Ooxoyozo (рис. 8.1, пунктир).
Можно рассматривать оси Ax1y1z1 как неподвижные при условии добавления к действительно приложенным силам только переносных сил инерции, так как оси Ax1y1z1 движутся поступательно. Если мы обозначим ускорение подвижного начала А через 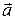 , то переносная сила, которую нужно приложить в каждой точке, будет
, то переносная сила, которую нужно приложить в каждой точке, будет 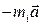 . Обозначим через ax, ay, az проекции ускорения
. Обозначим через ax, ay, az проекции ускорения 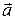 на оси Axyz. Тогда проекции переносной силы
на оси Axyz. Тогда проекции переносной силы 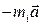 на те же оси будут
на те же оси будут 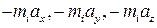 и сумма работ этих сил на возможном перемещении, сообщенном системе, будет равна
и сумма работ этих сил на возможном перемещении, сообщенном системе, будет равна
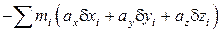 ,
,
где сумма распространена на все точки. Величины ax, ay, az являются известными функциями времени t. Полагая
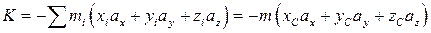 (8.6)
(8.6)
мы видим, что сумма виртуальных работ переносных сил равна 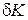 . При этом второе выражение для функции К получилось путем введения всей массы m системы и координат xC, yC, zC центра масс C относительно осей Axyz. Из него еще следует, что
. При этом второе выражение для функции К получилось путем введения всей массы m системы и координат xC, yC, zC центра масс C относительно осей Axyz. Из него еще следует, что
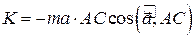 . (8.7)
. (8.7)
Благодаря введению этих переносных сил мы можем рассматривать оси Ax1y1z1 как неподвижные и применить уравнения Лагранжа к движению относительно этих осей, как если бы это движение было абсолютным. Обозначим через Т кинетическую энергию системы в движении относительно осей Ax1y1z1. Уравнения движения будут
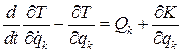 (8.8)
(8.8)
Слагаемое 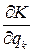 появляется вследствие добавления переносных сил инерции.
появляется вследствие добавления переносных сил инерции.
Действительно, виртуальная работа этих сил, равная δК, если выразить ее в функции переменных 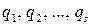 , имеет вид
, имеет вид
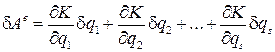 .
.
Если заданные силы имеют силовую функцию U, то
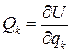
и правые части уравнений движения (8.6) можно написать в виде
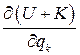 .
.
Вычисление величины Т. Скорость 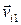 точки mi относительно осей Ax1y1z1, рассматриваемых как неподвижные, есть результирующая ее относительной скорости
точки mi относительно осей Ax1y1z1, рассматриваемых как неподвижные, есть результирующая ее относительной скорости 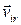 по отношению к осям Axyz и ее переносной скорости
по отношению к осям Axyz и ее переносной скорости 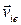 вместе с этими осями.
вместе с этими осями.
Проекции относительной скорости 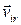 на оси Axyz равны производным
на оси Axyz равны производным 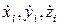 ; проекции
; проекции 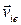 на те же оси равны
на те же оси равны 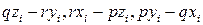 , так как при движении триэдра Axyz относительно осей Ax1y1z1 начало A неподвижно; здесь, как и раньше, р, q, r обозначают составляющие по осям Axyz мгновенной угловой скорости вращения
, так как при движении триэдра Axyz относительно осей Ax1y1z1 начало A неподвижно; здесь, как и раньше, р, q, r обозначают составляющие по осям Axyz мгновенной угловой скорости вращения 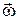 подвижного триэдра Axyz.
подвижного триэдра Axyz.
Следовательно, имеем:
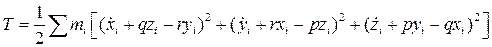
Положим:
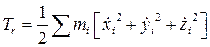 , (8.9)
, (8.9)
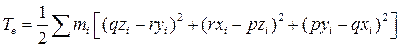 , (8.10)
, (8.10)
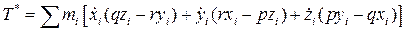 . (8.11)
. (8.11)
После этого можно написать
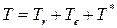 .
.
Величина Tr (8.9) есть кинетическая энергия системы в ее относительном движении относительно осей Axyz; она непосредственно выражается через переменные qk и их производные 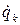 .
.
Величина Те (8.10) представляет собой кинетическую энергию системы, вызванную ее переносным вращением триэдра Axyz вокруг мгновенной оси Aw; она имеет, следовательно, выражение
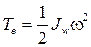 , (8.12)
, (8.12)
где Jw — момент инерции механической системы относительно оси Aw в момент t.
Наконец, Т* (8.11)можно переписать в виде
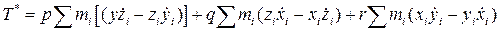 .
.
Вектор, 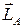 , проекции которого на подвижные оси равны
, проекции которого на подвижные оси равны
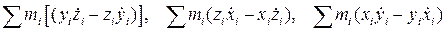 ,
,
есть главный момент относительно точки A количеств относительного движения 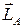 , и мы непосредственно имеем:
, и мы непосредственно имеем:
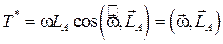 , (8.13)
, (8.13)
то есть эта часть кинетической энергии выражается через скалярное произведение вектора угловой скорости переносного вращения на вектор кинетического момента системы в относительном движении относительно начала подвижной системы координат.
Преимущество геометрических форм, которые мы дали величинам К, Tr, Te, T*, заключается в том, что в каждой конкретной задаче они непосредственно выражают эти величины в функции 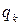 и
и 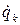 и нет необходимости прибегать к преобразованию координат.
и нет необходимости прибегать к преобразованию координат.
Пример.Рассмотрим неподвижную вертикальную ось Оу и плоскость Р, проходящую через эту ось и вращающуюся вокруг нее с постоянной угловой скоростью ω. Найти движение однородного тяжелого стержня, скользящего без трения по этой плоскости (рис. 8.2). Радиус инерции стержня при движении в плоскости P ‑ ρ.
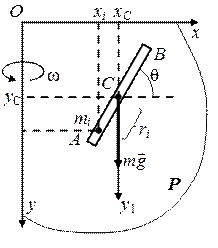
Рис. 8.2. Параметры движения стержня в плоскости Р
Требуется найти относительное движение стержня по отношению к осям Ох и Оу, проведенным в движущейся плоскости Р. Положение стержня относительно этих осей определяется тремя независимыми параметрами: координатами xC, yC центра тяжести C и углом θ между стержнем АВ и осью Ox.
Способ 1. На основе кинематики сложного движения точки. Абсолютная скорость какой-нибудь точки mi стержня есть результирующая ее относительной скорости, лежащей в плоскости хОу, и ее переносной скорости
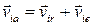 .
.
Эта последняя является скоростью, которой обладала бы точка mi, если бы она была неизменно связана с движущейся плоскостью. Следовательно, она равна ωхi, где xi — абсцисса точки mi, и перпендикулярна к плоскости хОу. Таким образом, переносная и относительная скорости взаимно перпендикулярны, и мы имеем
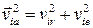 .
.
В таком случае для абсолютной кинетической энергии Та для уравнений (8.2) имеем
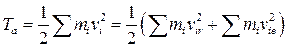
Вычислим оба члена отдельно. Относительное движение стержня является движением в плоскости хОу; кинетическая энергия в этом движении по теореме Кёнига будет
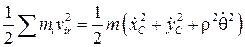
где 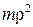 — момент инерции стержня относительно его центра масс C, ρ – его радиус инерции.
— момент инерции стержня относительно его центра масс C, ρ – его радиус инерции.
С другой стороны,
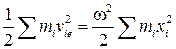 .
.
Сумма 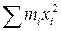 есть момент инерции стержня относительно оси Оу, который равен моменту инерции стержня
есть момент инерции стержня относительно оси Оу, который равен моменту инерции стержня 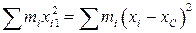 относительно параллельной оси вращения Оу оси Cy1, проходящей через центр масс С, увеличенному на произведение всей массы на квадрат расстояния между этими осями, т. е. увеличенному на
относительно параллельной оси вращения Оу оси Cy1, проходящей через центр масс С, увеличенному на произведение всей массы на квадрат расстояния между этими осями, т. е. увеличенному на 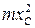 . Если через
. Если через 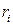 обозначить расстояние
обозначить расстояние 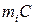 (рис. 8.2), то расстояние от какой-нибудь точки mk до этой центральной оси есть
(рис. 8.2), то расстояние от какой-нибудь точки mk до этой центральной оси есть 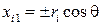 и сумма
и сумма 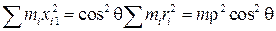 . Следовательно,
. Следовательно,
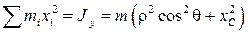
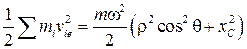 . (8.14)
. (8.14)
и абсолютная кинетическая энергия окончательно принимает вид
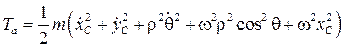 . (8.15)
. (8.15)
Так как единственной заданной силой является вес mg, приложенный в т. C, то существует силовая функция U = mgyC. Применяя последовательно уравнения Лагранжа к параметрам x, y, θ получим искомые уравнения движения. Итак,
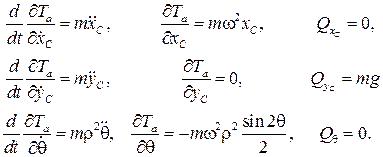 (8.16)
(8.16)
Сокращая на m, получим три уравнения движения, определяющие x, y, θ в функции t
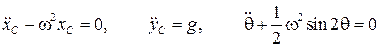 . (8.17)
. (8.17)
Способ 2. На основе принципа д’Аламбера. Согласно этому способу добавим к силам, действительно действующим на каждую точку mi переносные и кориолисовы силы инерции. На рис. 8.3 показана переносная сила инерции 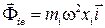 , приложенная к точке mi, и не показана кориолисова сила инерции, т.к. она перпендикулярна плоскости рисунка. После добавления таких сил составляются уравнения движения, как будто плоскость движения стержня неподвижна. Таким образом, кинетическая энергия стержня получит выражение как энергия в относительном движении – плоскопараллельном движении стержня
, приложенная к точке mi, и не показана кориолисова сила инерции, т.к. она перпендикулярна плоскости рисунка. После добавления таких сил составляются уравнения движения, как будто плоскость движения стержня неподвижна. Таким образом, кинетическая энергия стержня получит выражение как энергия в относительном движении – плоскопараллельном движении стержня
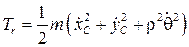 .
.
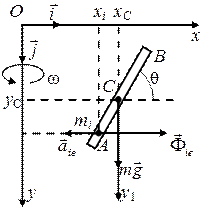
Рис. 8.3. К решению на основе принципа д’Аламбера
Поэтому
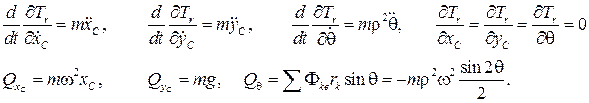 .
.
Уравнения приобретут вид, совпадающий с (8.17)
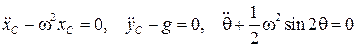 .
.
Дата добавления: 2015-10-21; просмотров: 1424;
