Лекция 10. Уравнения Лагранжа 1-го рода
Применяются при решении специальных задач. Прежде всего, их можно применить для определения реакций идеальных связей при движении системы. Достоинством уравнений Лагранжа 2-го рода является отсутствие в них реакций идеальных связей, что существенно облегчает задачу динамики и, вообще, делает ее разрешимой. Найти реакции идеальных связей в этом случае можно способом, основанным на применении принципа освобождаемости от связей. Сначала решается задача по определению законов изменения обобщенных координат, в которой реакции идеальных связей не учитываются. Затем механическая система разнимается по связям, реакции которых необходимо найти. Составляются уравнения Лагранжа 2-го рода для полученных в результате разъема связей частей системы. Туда подставляется найденное ранее решение и таким образом находится значение реакций связей.
Получим уравнения Лагранжа 1-го рода.
Имеем МС с l идеальными связями, уравнения которых
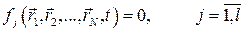 (10.1)
(10.1)
Отсюда, в соответствии с тем, что при варьировании время не меняется, а операция варьирования совпадает с операцией дифференцирования, получим
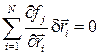 (10.2)
(10.2)
Умножим (10.2) на λj и сложим, получим
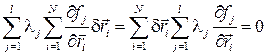 (10.3)
(10.3)
В то же время по свойству идеальности связей
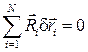 (10.4)
(10.4)
где 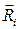 ‑ реакции идеальных связей.
‑ реакции идеальных связей.
Вычтем из уравнения (10.3) уравнение (10.4), получим
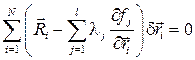 (10.5)
(10.5)
Среди 3N вариаций 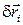 независимых вариаций будет только столько, сколько степеней свободы у МС, т.е. s. Остальные 3N-s , т.е. l будут зависимыми и выражаются через независимые из (10.2). Поэтому подберем значения коэффициентов λj так, чтобы выражения в скобках, куда они входят в уравнении (10.5), обращались в ноль. Остальные 3N-l=s скобок обязаны равняться нулю, т.к. при них стоят независимые вариации, а сумма (10.5) равна нулю при любых значениях этих вариаций. Таким образом, все скобки в выражении (10.5) равны нулю
независимых вариаций будет только столько, сколько степеней свободы у МС, т.е. s. Остальные 3N-s , т.е. l будут зависимыми и выражаются через независимые из (10.2). Поэтому подберем значения коэффициентов λj так, чтобы выражения в скобках, куда они входят в уравнении (10.5), обращались в ноль. Остальные 3N-l=s скобок обязаны равняться нулю, т.к. при них стоят независимые вариации, а сумма (10.5) равна нулю при любых значениях этих вариаций. Таким образом, все скобки в выражении (10.5) равны нулю
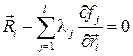 .
.
Откуда, находятся все силы реакций идеальных связей
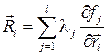 .
.
Запишем теперь уравнения движения всех точек системы, исходя из ІІ закона Ньютона
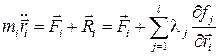 (10.6)
(10.6)
Это и есть уравнения Лагранжа I рода.
В этих 3N уравнениях 3N+l неизвестных, поэтому к ним следует добавить l уравнений связей (10.1).
Пример.
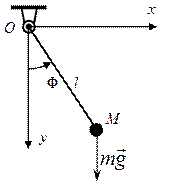
Рассмотрим пример малых движений математического маятника (рис. 8.1а).
| 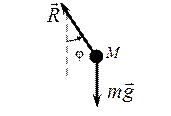
|
а б
Рис. 10.1.
Выбрав за обобщенную координату угол поворота оси невесомой нити от вертикали φ, получим
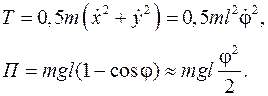
Тогда, согласно уравнениям Лагранжа 2-го рода (5.1), получим
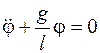 . (10.7)
. (10.7)
Откуда находим
 . (10.8)
. (10.8)
Теперь разрежем нить (освободим точку М от связи) и составим уравнение для точки М, движущейся под действием силы тяжести и силы натяжения нити (рис. 10.1б). Проектируем уравнение движения точки в форме 2-го закона Ньютона на нормаль, получаем
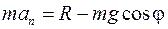 ,
,
Откуда,
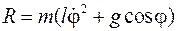 . (10.9)
. (10.9)
Для одновременного получения закона движения механической системы и действующих в ней реакций связей и служат уравнения Лагранжа 1-го рода.
Составим уравнения движения математического маятника в форме уравнений Лагранжа 1-го рода
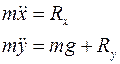 (10.10)
(10.10)
Выразим проекции силы реакции связи через неопределенные множители Лагранжа


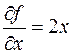 ,
, 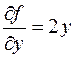 ,
,
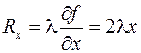 ,
,  ,
,
получим уравнения (10.10) в виде
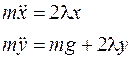
Найдем из первого 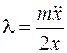 , подставим во второе, получим
, подставим во второе, получим
 . (10.11)
. (10.11)
Это уравнение решается заменой
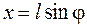 ,
, 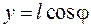 . (10.12)
. (10.12)
получим уравнение (10.7). Но, одновременно,
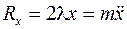
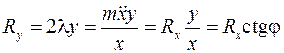 .
.
После подстановки в первое уравнение заменяющей формулы (10.12) и уравнения (10.7), окончательно, получим
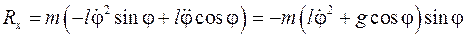
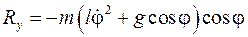 ,
,
что совпадает с решением (10.9).
Дата добавления: 2015-10-21; просмотров: 2863;
