Лекция 11. Конфигурационные многообразия.

Конфигурационное многообразие. Для получения наглядного геометрического образа обсуждаемых здесь вопросов введем понятие конфигурационного многообразия. Представим себе (n=3N)-мерное эвклидово пространство, где N – число точек МС. Тогда МС будет отображаться в нем некоторой точкой S с координатами X₁, Y₁, Z₁, X₂, Y₂, Z₂,…, X_N, Y_N, Z_N, которые переобозначим x₁=X₁, x₂=Y₁, x₃=Z₁, x₄=X₂, x₅=Y₂, x₆=Z₂,…, x_n-2=X_N, x_n-1=Y_N, x_n=Z_N.. Наличие l голономных реономных (нестационарных) связей c уравнениями вида (4.6) задает в таком пространстве перемещающуюся гиперповерхность S_t (рис.11.1).

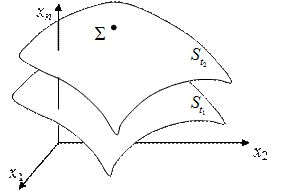
Рис. 11.1

МС отображается в таком случае точкой (S) на многообразии. В случае склерономности (стационарности) связей это многообразие будет неподвижным. Технология аналитической механики при построении математических моделей использует «остановленные» многообразия, описываемые уравнениями (4.6) при фиксированном значении времени t. Поэтому остановленное многообразие S_t в механике называется конфигурационным многообразием системы S. 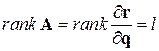Если l уравнений (4.6) ( , i=1,2,…,N, j=1,2,…,l) независимы, о чем свидетельствует условие (2.17) ( ), то размерность конфигурационного многообразия s=3N-l.

Уравнения s-мерного многообразия можно задать параметрически в виде (5.3) ( 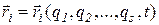), используя криволинейные координаты ‑ обобщенные координаты q={q₁, q₂,…, q_s}. Фиксируя все обобщенные координаты, кроме одной, можно получить координатные линии s_k (k=1,2,…,s) на многообразии (рис. 8.2) и построить локальный базис многообразия

.

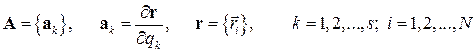Этот базис составляется из векторов 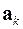, которые должны быть линейно независимыми. Критерием этого есть условие

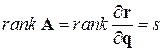. (11.1)

Рис. 11.2.

Такой базис на конфигурационном многообразии образует гиперплоскость – карту. Естественно, в другом положении МС условие (11.1) для данного набора обобщенных координат может быть не выполнено, поэтому там, возможно, следует заменить набор обобщенных координат, т.е. работать с другой картой. Совокупность таких карт образует атлас многообразия.

Тут аналогией является атлас карт земной поверхности, в котором, очевидно, что описывать экваториальные области можно в угловых координатах параллель-меридиан, а в полярной области ‑ использовать декартовые координаты с началом в центре Земли (рис. 11.3). Например, для обобщенных координат y, q радиус-вектор точки земной поверхности запишется через декартовые координаты в виде

.

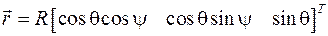Тогда все миноры 2-го порядка матрицы критерия (7.1)

, (11.2)

равные при 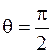одновременно обращаются в нуль.

Рис. 11.3.