Способ 3. Метод Жильбера.

Если придерживаться буквально технологии метода Жильбера, то надо ввести в рассмотрение дополнительную систему координат, начало которой совпадает с началом подвижной системы координат, и которая должна двигаться поступательно относительно неподвижной системы. Так как начало подвижной системы координат в этой задаче (т. О на рис. 8.2) есть неподвижная точка, то эта дополнительная система координат будет неподвижной и совпадать с абсолютной неподвижной системой. Покажем, что уравнения движения стержня, полученные методом Жильбера, будут совпадать с ранее полученными уравнениями (8.12).

Будем считать, что поступательно движущаяся система координат, обозначенная на рис. 8.1 Ax₁y₁z₁, здесь будет неподвижной СК Ox_Oy_O (рис. 8.4). В связи с этим, форма K (8.6) будет равна нулю. Определим формы (8.9)-(8.11). Первая по-прежнему равна

.

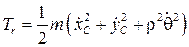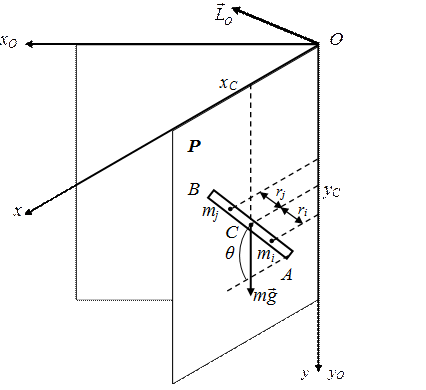
Рис. 8.4.

Вторая в форме (8.12) уже вычислена (см. формулу (8.14))

.

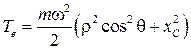Третья (8.11) в форме (8.13) будет тождественно равна нулю, т.к. вектор кинетического момента 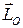при плоскопараллельном движении стержня в плоскости Р будет перпендикулярным угловой скорости .

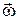Таким образом, кинетическая энергия приобретет вид (8.15). Среди действующих сил в этом случае учитывается только сила тяжести стержня (начало координат системы Ox_Oy_O неподвижно, поэтому переносная сила инерции равна нулю), поэтому обобщенные силы получатся в виде, как в формулах (8.16). В связи с совпадением выражений производных кинетической энергии и обобщенных сил с выражениями (8.16), уравнения движения также совпадут с формулами (8.17).