Применение метода Рунге-Кутта четвёртого порядка для численного решения нормальных систем ОДУ.

Метод Рунге-Кутта для нормальных систем рассмотрим на примере задачи Коши для нормальной системы ОДУ второго порядка:

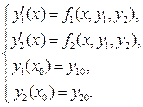
Далее вычислительную схему метода Рунге-Кутта (36) будем применять отдельно к каждому уравнению данной нормальной системы. При этом частные приращения для первой искомой функции y₁(x), рассчитываемые в соответствии с правилом (36), будем обозначать через 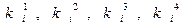, а частные приращения для второй искомой функции y₂(x) будем обозначать как .

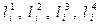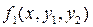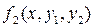Поскольку правые части уравнений нашей системы ОДУ, т.е. функции и зависят от обеих искомых функций y ₁(x) и y₂ (x), то приращения для y ₁(x) и y₂ (x) на каждом шаге метода вычисляются одновременно. Поэтому метод Рунге-Кутта четвёртого порядка для решения задачи Коши для нормальной системы ДОУ второго порядка имеет вид:

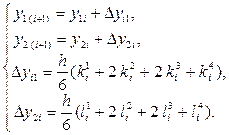
где:

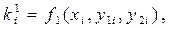
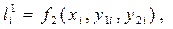
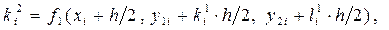
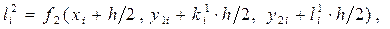
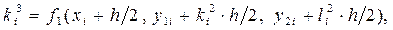
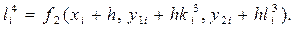
§6. Разностные аппроксимации задачи Коши.

6.1 Разностный способ решения задачи Коши.

В отличие от рассмотренных выше методов разностный способ решения задачи Коши основан на замене (т.е. на аппроксимации) входящей в ДУ производной y¢(x) каким-либо разностным отношением, т.е. на использовании формул аппроксимаций производной, рассмотренных ранее при изучении численного дифференцирования [1, стр. 590].

Как и раньше рассмотрим задачу Коши для ОДУ в её обычной формулировке:

y¢(x) = f (x, y(x)), xÎ [x₀, b] (1)

y (x₀) = y ₀ (2)

Речь идёт о получении числовой таблицы (табл. 1) приближённых значений
y_i » y(x_i) искомого решения y(x) задачи Коши на сетке x _i Î [x₀, b] с шагом 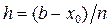, при этом расчётными точками метода (узлами) служат точки
x _i = x₀ + ih (i = 0,1, …, n).

Таблица 1приближённые значения решения

Иногда задаваемую таблицей 1 совокупность приближённых решений задачи Коши: y₀» y(x₀), y₁» y(x₁), y₂» y(x₂), …, y_n » y(x_n) также называют каркасом решений,соответствующим узлам сетки

w_h º {x _i|x _i = x₀ + ih (i = 0,1, …, n)}.

Применительно к начальным значениям x₀ и y₀ , задающим начальные условия (2), уравнение (1) превращается в равенство:

y¢ (x₀) = f (x₀, y(x₀) ) º f (x₀,y₀). (37)

Воспользуемся результатами, полученными при численном дифференцировании функций, (лекция 4) и применим к левой части равенства (37) аппроксимацию производной правым разностным отношением первого порядка:

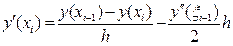, где x _i+1 Î(x _i; x_i+1). (38)

которое в точке x₀, т.е. при i = 0, приобретает вид:

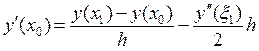, где x₁ Î(x₀; x₁). (39)

При использования аппроксимации (39) для производной 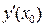соотношение (37) перепишется в виде:

.

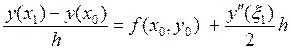Откуда получаем формулу для вычисления точного значения решения y(x) в узле x₁:

, (40)

Опуская в формуле (40) слагаемое 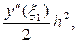характеризующее ошибку используемой аппроксимации производной, мы получим формулу для вычисления приближённого значения y₁ решения y(x₁) в узле x₁:

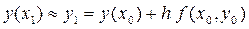, (41)

которая идентична выражению, полученному на первом шаге вычислительной процедуры при использовании метода ломаных Эйлера: y₁ = y₀ + h f (x₀, y₀).

Понятно, что для получения общей расчётной формулы для вычисления приближённых значений y_i решения y(x_i), аналогичной соотношению (41), в равенстве:

y¢ (x_i) = f (x_i, y(x_i) ) (42)

необходимо использовать аппроксимацию для производной y¢(x_i) на основе формулы (38):

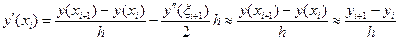(43)

заменив при этом неизвестное точное значение y(x_i), полученным на основе пошаговой вычислительной процедуры известным приближённым значением y_i. В результате получим формулу для вычисления приближённого значения y_i+1 решения y(x_i+1) в узле x_i+1:

y_i+1 = y_i + h f (x_i, y_i).

Порядок точностиполучающегося таким образом «разностногометода» численного интегрирования задачи Коши(1), (2) совпадает с порядком точности аппроксимации производной исходного дифференциального уравнения.

Знание порядков используемых формул аппроксимаций производной и их остаточных членов позволяет выводить оценки погрешностей приближённых решений задачи Коши (на используемой сетке) и изучать устойчивость и сходимость получаемых каркасов решений.

В связи с использованием разностных отношений для построения моделей дифференциальных уравнений, такие модели называются разностными уравнениями или разностными схемами.