Методы решения задачи Коши с помощью формулы Тейлора
Эйлеру принадлежит идея построения численных методов, основанных на возможности получить разложение искомого решения y(x) в ряд Тейлора в окрестности требуемого значения аргумента x = xi:
y(x) = y(xi) + 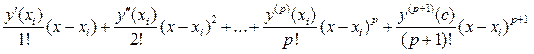
при этом значение первой производной y¢(x) находят из самого дифференциального уравнения y¢(x) = f (x, y), а производные, y¢¢(xi), y¢¢¢(xi), …, y(p)(xi) можно найти, дифференцируя функцию f (x, y(x)) нужное число раз.
§2. Исправленный метод Эйлера.
Рассмотрим задачу Коши для ОДУ первого порядка:
| y¢(x) = f (x, y), xÎ(r1, r2) = [x0, b] y (x0) = y0 | (1) (2) |
Вычислительная задача состоит в поиске приближённых значений решения y(x) задачи Коши на некоторой сетке равноотстоящих узлов. Способ получения приближённого решения основан на разложении (в окрестности некоторого узла xi) искомого решения y(x) ДУ (1) в ряд Тейлора с последующей заменой присутствующих в таком разложении величин y(xi), y¢(xi), y¢¢(xi) … их приближёнными значениями.
Пусть (каким-либо способом) уже найдено приближённое значение yi » y(xi) решения y(x) данной задачи Коши в узле xi и требуется вычислить приближённое значение yi+1 решения y(x) в узле xi+1:
yi+1» y (xi+1), x i+1 = x i + h.
В окрестности точки xi запишем разложение точного решения y(x) задачи Коши (1), (2) в ряд Тейлора p - го порядка с остаточным членом в форме Лагранжа:
y(x) = y(xi) + 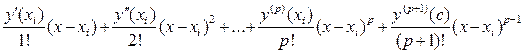 (3)
(3)
где при постоянном p и x ® xi величина 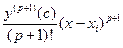 является бесконечно малой порядка p + 1 в сравнении с величиной
является бесконечно малой порядка p + 1 в сравнении с величиной 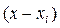 .
.
Полагая далее в разложении (3), что x = xi+1 получим:
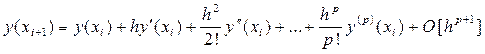 (4)
(4)
где 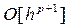 =
= 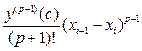 величина бесконечно малая порядка p + 1 в сравнении с шагом сетки h.
величина бесконечно малая порядка p + 1 в сравнении с шагом сетки h.
Учёт линейных по h слагаемых в разложении решенияy(x). Ограничимся двумя слагаемыми в разложении (4), что соответствует случаю p = 1, тогда из (4) получим:
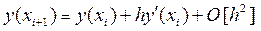 , (5)
, (5)
и учитывая, что y¢(xi) = f (xi,y(xi)), получим выражение:
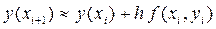 , i = 0, 1, …, n (6)
, i = 0, 1, …, n (6)
которое совпадает в формулой, определяющей пошаговый метод Эйлера.
Пошаговая ошибка метода интегрирования задачи Коши. Из формулы (5) следует, что остаточный член 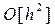 характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т.е. ошибку, совершаемую на одном шаге вычисления. Очевидно, что от шага к шагу, т.е. при многократном применении формулы (5) для
характеризует локальную (или, иначе, шаговую) ошибку метода Эйлера, т.е. ошибку, совершаемую на одном шаге вычисления. Очевидно, что от шага к шагу, т.е. при многократном применении формулы (5) для
i = 0, 1, …, n возможно наложение ошибок. За n – шагов применения метода Эйлера, т.е. в точке x = b, образуется (накапливается) глобальная ошибка метода. Таким образом, порядком глобальной ошибки характеризуется порядок точности соответствующего численного процесса решения задачи Коши.
Изучение и оценка глобальной ошибки метода Эйлера будет приведено ниже. Здесь без доказательства, приведём утверждение [1, стр. 539], позволяющее оценивать глобальную ошибку вычислительного процесса и установить её связь с локальной (т.е. пошаговой) ошибкой метода.
Утверждение*. Порядок глобальной ошибки численного процесса (относительно шага h) на единицу меньше, чем порядок локальной ошибки метода.
В соответствии с (5) формула Эйлера соответствует линейному (по h) фрагменту разложения решения y(x) в ряд Тейлора в окрестности точки xi, следовательно, шаговая или локальная погрешность метода Эйлера (т.е. погрешность, допускаемая на каждом шаге реализации метода) имеет порядок 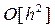 , т.е. имеет порядок отброшенного остаточного члена. Поэтому в соответствии с утверждением* глобальная ошибка метода Эйлера на единицу меньше, чем порядок локальной ошибки метода, т.е. метод Эйлера относится к методам первого порядка по h.
, т.е. имеет порядок отброшенного остаточного члена. Поэтому в соответствии с утверждением* глобальная ошибка метода Эйлера на единицу меньше, чем порядок локальной ошибки метода, т.е. метод Эйлера относится к методам первого порядка по h.
Учёт квадратичных слагаемых по h в разложении решения y(x). Далее при p = 2 из формулы (4) следует равенство:
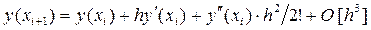 , (6)
, (6)
которое представляет собой метод нахождения решения y(xi+1) с шаговой погрешностью 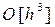 . В формуле (6) фигурируют неизвестные величины y¢(xi) и y¢¢(xi). Поэтому дальнейшая задача состоит в замене неизвестных значений y¢(xi) и y¢¢(xi) их приближёнными значениями, полученными на основе исходного ДУ.
. В формуле (6) фигурируют неизвестные величины y¢(xi) и y¢¢(xi). Поэтому дальнейшая задача состоит в замене неизвестных значений y¢(xi) и y¢¢(xi) их приближёнными значениями, полученными на основе исходного ДУ.
Поскольку считаем, что нам известно приближённое значение yi » y(xi) решения y(xi) в точке xi, то из (1) находим приближённое значение первой производной y¢(xi) в точке xi:
y¢(xi) = f (xi, y(xi) ) » f (xi, yi), (7)
где yi приближённое значение решения y(x) в точке xi, т.е. yi » y(xi).
Для нахождения приближённого значения величины y¢¢(xi) продифференцируем исходное ДУ (1) по формуле полной производной:
y¢¢(x) = f¢ (x, y(x)) = 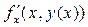 = f¢x(x, y(x)) + f¢y(x, y(x)) y¢. (8)
= f¢x(x, y(x)) + f¢y(x, y(x)) y¢. (8)
Напомним, что полным дифференциалом или приращением функции f (x, y) двух переменных x и y называется выражение:
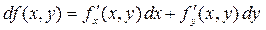 , (9)
, (9)
где 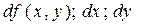 - соответственно дифференциалы, т.е. приращения функции
- соответственно дифференциалы, т.е. приращения функции
f (x, y) и переменных x и y.
Разделив левую и правую части выражения (9) на величину дифференциала dx, получаем:
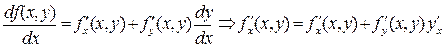 (10)
(10)
Таким образом, доказана, справедливость выражения (8).
Из выражения (8) заменяя y(xi) на yi находим приближённое значение второй производной решения y¢¢(x) в точке xi:
y¢¢(xi) = f¢x (xi, y(xi)) + f¢y (xi, y(xi)) f (xi, y(xi)) Þ
y¢¢(xi) » f¢x (xi, yi) + f¢y (xi, yi) f (xi, yi) (11)
Таким образом, получена следующая совокупность соотношений (12) для приближённых значений решения y(x), его первой и второй производной в точке xi:
| y(xi) » yi; y¢(xi) = f (xi, y(xi)) » f (xi, yi ); y¢¢(xi) » f¢x (xi, yi) + f¢y (xi, yi) f (xi, yi). | (12) |
Подставляя соотношения (12) в разложение (6) получаем формулу для вычисления приближённого значения решения yi+ 1» y(xi+ 1) при i = 0, 1, …, n:
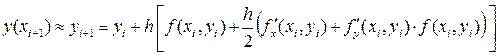 (13)
(13)
Определяемый формулой (13) алгоритм называется исправленнымметодом Эйлера.
Отметим, что в силу начального условия y0 = y(x0) формулы (7) и (11) для y¢(xi) и y¢¢(xi) при i = 0, являются точными, поэтому для значения y1» y(x1), полученного на первом шаге вычислений по формуле (13), будет совершаться ошибка, связанная только с «усечением» ряда Тейлора, т.е. с отбрасыванием его остаточного члена. Следовательно, локальная ошибка или шаговая погрешность метода (13) составляет величину 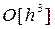 .
.
Дата добавления: 2015-09-14; просмотров: 3181;
