Мощность множества

Говорят, что А и В имеют одинаковую мощность, если существует взаимно-однозначное (1:1) отображение множества А на множество В (несколько позже мы поясним, чтó это означает).

Конечные множества имеют одинаковую мощность тогда и только тогда, когда они состоят из одного и того же числа элементов. Для конечных множеств одинаковой мощности из условия А Ì В всегда следует, что А = В. Для бесконечных множеств это может быть не так. Выпишем, например, множество натуральных чисел и его подмножество – множество четных чисел:

1 2 3 4 5…

2 4 6 8 10…

Каждому элементу верхнего ряда сопоставим соответствующий элемент нижнего ряда:

n ® 2n.

Это – взамно-однозначное отображение одного множества на другое. Значит, они равномощны, хотя и не совпадают.

Счетным называется множество, имеющее ту же мощность, что и множество натуральных чисел. Таким образом, все элементы счетного множества А можно «пересчитать» с помощью натурального ряда, т.е. указать 1:1 соответствие 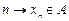, не пропустив при этом ни одного элемента из А. Несколько неожиданный факт состоит в том, что множество всех рациональных чисел счетно (попробуйте сообразить, как можно «пересчитать» рациональные числа). Таким образом, рациональных чисел оказывается «столько же», сколько и натуральных (хотя, на первый взгляд, рациональных чисел гораздо больше: ведь между любыми двумя вещественными числами имеется рациональное и, следовательно, рациональные числа плотно расположены на числовой оси, чего не скажешь о натуральных числах). Говорят, что множество всех чисел на отрезке [0, 1] имеет мощность континуум. Такую же мощность имеет множество úвсех вещественных чисел, а также множество всех иррациональных чисел.

В определенном смысле множество рациональных чисел представляет собой очень «незначительную часть» множества вещественных чисел (несмотря на то, что любое иррациональное число можно сколь угодно точно приблизить последовательностью рациональных).

Возникает вопрос: существуют ли множества промежуточной мощности между мощностью счетного множества и мощностью континуума? (Отрицательный ответ на этот вопрос носит название «континуум-гипотезы»). Этот вопрос оказался очень трудным и долгое время оставался без ответа. Ответ был найден П. Коэном в 1963 году и оказался удивительным: континуум-гипотеза неразрешима – ее невозможно ни доказать, ни опровергнуть, можно лишь принять ее или противоположное ей утверждение как аксиому, которая не будет (при любом возможном выборе) противоречить другим аксиомам математики. К счастью, нам не придется сталкиваться с ситуациями, в которых требуется делать подобный выбор.