Сюръекция, инъекция, биекция

 Говорят, что f отображает X на Y (и пишут
Говорят, что f отображает X на Y (и пишут 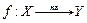 ), если область значений Y совпадает с f(Х), т.е. Y = f(Х). Это означает, что для любого y Î Y найдется х Î Х такой, что y = f(x) (т.е. у любого
), если область значений Y совпадает с f(Х), т.е. Y = f(Х). Это означает, что для любого y Î Y найдется х Î Х такой, что y = f(x) (т.е. у любого
y Î Y $ прообраз х). Отображение «на» называют также сюръективным, или сюръекцией, от французского «sur» – «на».



 Говорят, что отображение f: X ® Y взаимно-однозначно (1:1) (и пишут
Говорят, что отображение f: X ® Y взаимно-однозначно (1:1) (и пишут 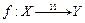 ), если из условий
), если из условий 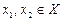 ,
, 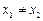 следует, что
следует, что 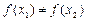 , т.е. различным значениям аргумента соответствуют различные значения функции (в этом случае каждый образ имеет не более одного прообраза). Взаимно-однозначное отображение называют также инъективным, или инъекцией.
, т.е. различным значениям аргумента соответствуют различные значения функции (в этом случае каждый образ имеет не более одного прообраза). Взаимно-однозначное отображение называют также инъективным, или инъекцией.
Пусть X и Y – подмножества числовой оси. В этом случае f: X ® Y есть числовая функция числового аргумента. Для нее взаимная однозначность вытекает из монотонности. Напомним, что функция называется монотонно возрастающей на отрезке [а, b], если из условий 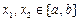 ,
, 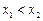 вытекает, что
вытекает, что 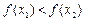 . Аналогично определяется монотонно убывающая на отрезке функция (определите). Функция монотонна на отрезке, если она монотонно возрастает или монотонно убывает на этом отрезке.
. Аналогично определяется монотонно убывающая на отрезке функция (определите). Функция монотонна на отрезке, если она монотонно возрастает или монотонно убывает на этом отрезке.
УТВЕРЖДЕНИЕ.Монотонная функция является взаимно-однозначной. (Докажите это утверждение).
Отображение 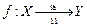 , являющееся сюръективным и инъективным одновременно, называется биективным, или биекцией («би» – «два»). Итак, биекция = инъекция + сюръекция.
, являющееся сюръективным и инъективным одновременно, называется биективным, или биекцией («би» – «два»). Итак, биекция = инъекция + сюръекция.
Дата добавления: 2015-09-14; просмотров: 1820;
