Основные элементарные функции. 1) степенная функция ; 2) показательная функция (а > 0, а ¹ 1); 3) логарифмическая функция (напомним
К ним относятся:
| 1) степенная функция | 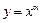 ; ;
|
| 2) показательная функция | 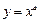 (а > 0, а ¹ 1); (а > 0, а ¹ 1);
|
3) логарифмическая функция
(напомним, что при х > 0 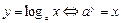 , т.е. логариф-мическая функция является обратной к показательной); , т.е. логариф-мическая функция является обратной к показательной);
| 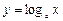 (а > 0, а ¹ 1) (а > 0, а ¹ 1)
|
| 4) тригонометрические функции | sin x, cos x, tg x, ctg x; |
| 5) обратные тригонометрические функции | arcsin x, arccos x, arctg x, arcctg x. |
Функция называется элементарной, если она образована из основных элементарных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и конечного числа операций взятия функции от функции – суперпозиций. Например, элементарной является функция 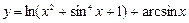 .
.
Дата добавления: 2015-09-14; просмотров: 500;
