Последовательность и ее предел
Пусть имеется правило, по которому каждому натуральному n ставится в соответствие вещественное число 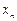 :
: 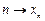 . В этом случае говорят, что задана последовательность
. В этом случае говорят, что задана последовательность 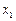 ,
, 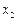 ,… Коротко ее обозначают
,… Коротко ее обозначают 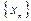 . При этом число
. При этом число 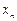 называют n-м членом, или общим членом, последовательности
называют n-м членом, или общим членом, последовательности 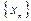 .
.
Примеры:
а) 1, 2, 3, 4, 5,… Здесь 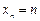 . Для нее
. Для нее 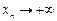 . (Чтó это значит, мы определим позже).
. (Чтó это значит, мы определим позже).
б) – 1, – 2, –3,…, т.е. 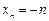 . Для нее
. Для нее 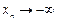 .
.
в) –1, 2, – 3, 4, –5, 6,… Þ 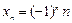 . Здесь
. Здесь 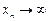 (без знака!).
(без знака!).
г) 1, 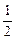 ,
, 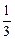 ,
, 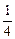 ,
, 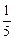 ,… Þ
,… Þ 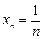 . Здесь
. Здесь 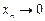 (запомните!), точнее
(запомните!), точнее 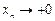 (стремится к нулю справа, оставаясь положительным).
(стремится к нулю справа, оставаясь положительным).
д) 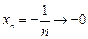 (стремится к нулю слева).
(стремится к нулю слева).
е) – 1, 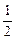 ,
, 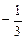 ,
, 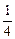 ,
, 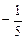 ,…Þ
,…Þ 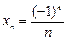 . Здесь
. Здесь 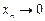 (без знака).
(без знака).
ж) –1, 1, –1, 1, –1, 1,… 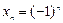 . Эта последовательность никуда не стремится (хотя и ограничена).
. Эта последовательность никуда не стремится (хотя и ограничена).
з) 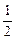 ,
, 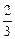 ,
, 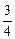 ,
, 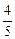 ,
, 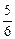 ,… Þ
,… Þ 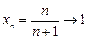 , т.к.
, т.к.
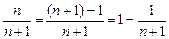 , а
, а 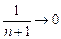 .
.
Итак, 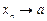 , если
, если 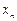 «неограниченно приближается» к а с ростом n. Формальное определение таково:
«неограниченно приближается» к а с ростом n. Формальное определение таково: 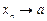 при n ® ¥, или, что то же самое,
при n ® ¥, или, что то же самое, 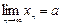 , если "e > 0 $N = N(e) такое, что
, если "e > 0 $N = N(e) такое, что 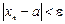 "n > N.
"n > N.
Другими словами, 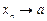 (
( 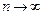 ), если для любой окрестности точки а найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности (поясните эквивалентность определений).
), если для любой окрестности точки а найдется номер, начиная с которого все члены последовательности принадлежат этой окрестности (поясните эквивалентность определений).
УПРАЖНЕНИЕ.Докажите, что
а) 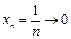 при
при 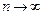 ; б)
; б) 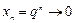 при
при 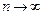 , если
, если 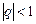 .
.
Говорят, что последовательность 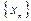 монотонно возрастает (не убывает), если
монотонно возрастает (не убывает), если 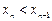 "n (
"n ( 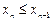 "n).
"n).
Говорят, что последовательность 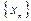 ограничена сверху, если
ограничена сверху, если
$М > 0 такое, что 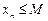 "n.
"n.
Аналогично определяются монотонно убывающая (не возрастающая) последовательность и последовательность, ограниченная снизу.
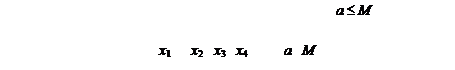








 ТЕОРЕМА. Монотонно возрастающая (или даже неубывающая) ограниченная сверху последовательность имеет конечный предел.
ТЕОРЕМА. Монотонно возрастающая (или даже неубывающая) ограниченная сверху последовательность имеет конечный предел.
Другими словами, если для всех n 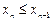 и
и 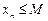 , то
, то 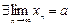 и
и 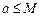 .
.
Аналогичное утверждение справедливо и для монотонно убывающей (не возрастающей) ограниченной снизу последовательности (сформулируйте его).
6. Число е
Рассмотрим последовательность 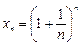 . Имеем:
. Имеем:
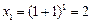 ,
, 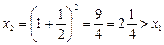 ,
,
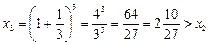 ,
,
и т.д. Можно показать, что 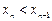 "n и что
"n и что 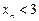 "n. Следовательно, существует предел этой последовательности, обозначаемый е:
"n. Следовательно, существует предел этой последовательности, обозначаемый е:
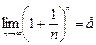 .
.
Это обозначение предложил Л. Эйлер (Euler, 1707–1783), великий математик, родившийся в Швейцарии и работавший в России.
Число е играет в математике не менее важную роль, чем p ( в этом мы не раз убедимся). Приближенно оно равно 2,7. Более точное значение таково: е = 2,718281828… Год рождения Л. Толстого (1828) стоит здесь дважды подряд, но не является периодом, т.к. число е иррационально (дальнейшие цифры 4590…). Заметим также, что 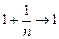 , в то время как показатель степени
, в то время как показатель степени 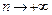 . Таким образом,
. Таким образом, 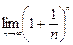 есть «неопределенность» типа
есть «неопределенность» типа 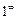 .
.
Если в этом пределе величину 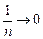 заменить нулем, то в пределе получим единицу, поскольку единица в любой степени есть единица. Если же
заменить нулем, то в пределе получим единицу, поскольку единица в любой степени есть единица. Если же 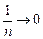 заменить любой сколь угодно малой, но фиксированной положительной величиной, то в пределе получим + ¥. Более того, + ¥ мы получим и в том случае, когда заменим
заменить любой сколь угодно малой, но фиксированной положительной величиной, то в пределе получим + ¥. Более того, + ¥ мы получим и в том случае, когда заменим 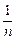 на величину
на величину 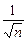 , также стремящуюся к нулю, но медленнее, чем
, также стремящуюся к нулю, но медленнее, чем 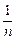 (либо заменим показатель степени n на быстрее растущую величину
(либо заменим показатель степени n на быстрее растущую величину 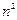 ). Заменив же величину
). Заменив же величину 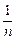 на величину
на величину 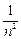 , быстрее стремящуюся к нулю (или показатель степени п на показатель
, быстрее стремящуюся к нулю (или показатель степени п на показатель 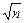 ), мы получим в пределе 1. В этом предлагается убедиться самостоятельно или с помощью преподавателя на практических занятиях. Там же вы увидите, что неопределенность типа
), мы получим в пределе 1. В этом предлагается убедиться самостоятельно или с помощью преподавателя на практических занятиях. Там же вы увидите, что неопределенность типа 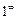 может давать и любые другие ответы между 1 и + ¥. С неопределенностями других типов мы еще не раз встретимся при вычислении пределов.
может давать и любые другие ответы между 1 и + ¥. С неопределенностями других типов мы еще не раз встретимся при вычислении пределов.
Функция 
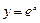 называется экспонентой и обозначается exp(x).
называется экспонентой и обозначается exp(x).
Логарифм с основанием е называется натуральным логарифмом и обозначается ln x:
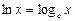 .
.



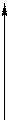


 (Напомним, что
(Напомним, что 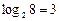 , поскольку
, поскольку 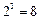 ).
).
ЛЕКЦИЯ 2. ФУНКЦИЯ, ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
Дата добавления: 2015-09-14; просмотров: 574;
