Тема 1.4. Плоская система произвольно расположенных сил.
1.4.1. Параллельный перенос силы. Теорема Пуансо.
1.4.2. Приведение плоской системы сил к одному центру. Главный вектор и главный момент системы сил.
1.4.3. Условия равновесия произвольной плоской системы сил.
1.4.4. Различные формы уравнений равновесия произвольной плоской системы сил.
1.4.1. Теорема Пуансо.Не изменяя действия силы на тело её можно переносить параллельно своему начальному направлению в любую точку тела, присоединяя при этом некоторую пару сил.
Параллельный перенос силы является не только весьма плодотворным формальным приёмом, но в ряде случаев соответствует и физической сущности явлений.
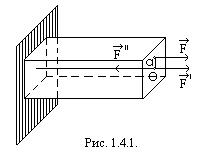 В качестве примера рассмотрим брус, на который действует сила
В качестве примера рассмотрим брус, на который действует сила 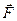 , приложенная перпендикулярно к поперечному сечению бруса на расстоянии
, приложенная перпендикулярно к поперечному сечению бруса на расстоянии 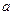 от центра О тяжести этого сечения (рис. 1.4.1.).
от центра О тяжести этого сечения (рис. 1.4.1.).
Приложим в точке О уравновешенную систему сил 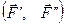 таких, что
таких, что 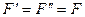 . Тогда действие на брус данной (внецентренной) силы
. Тогда действие на брус данной (внецентренной) силы 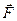 эквивалентно действию на него силы
эквивалентно действию на него силы 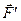 , проходящей через центр О и растягивающей брус, и пары
, проходящей через центр О и растягивающей брус, и пары 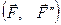 с моментом
с моментом 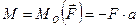 , изгибающей брус.
, изгибающей брус.
Вполне возможно и обратное действие: силу и пару, лежащие в оной плоскости, всегда можно заменить одной силой, равной данной силе, перенесённой параллельно своему начальному направлению в некоторую другую точку.
В самом деле, данную силу всегда можно перенести параллельно своему начальному направлению в такую точку, чтобы добавляемая при этом пара имела момент, равный по абсолютному значению, но противоположный по знаку моменту данной пары. Тогда эти две пары взаимно уравновесятся и у нас останется только одна сила, равная по модулю данной, одинаково с ней направленная, но имеющая другую линию действия.
1.4.2. 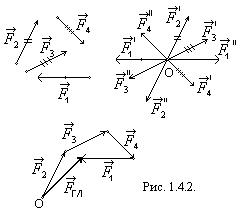 Пусть имеем систему нескольких, например четырёх, сил
Пусть имеем систему нескольких, например четырёх, сил 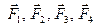 , расположенных как угодно на плоскости (рис. 1.4.2.).
, расположенных как угодно на плоскости (рис. 1.4.2.).
Возьмём в плоскости действия сил произвольную точку О. Назовём эту точку центром приведения и поочерёдно приведём к ней, пользуясь теоремой Пуансо, все данные силы. В результате приведения получим систему сил 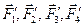 , приложенных в этой точке, и систему пар
, приложенных в этой точке, и систему пар 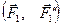 ,
, 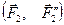 ,
, 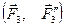 ,
, 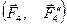 .
.
Приложенные в одной точке О силы 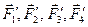 мы можем сложить по правилу силового многоугольника и, следовательно, заменить одной эквивалентной им силой
мы можем сложить по правилу силового многоугольника и, следовательно, заменить одной эквивалентной им силой 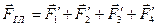 , равной их геометрической сумме. Так как
, равной их геометрической сумме. Так как 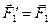 ,
, 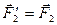 ,
, 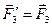 ,
, 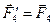 , то
, то 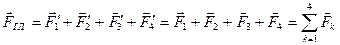 . Вектор
. Вектор 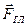 , равный геометрической сумме всех сил данной системы, является главным векторомэтой системы:
, равный геометрической сумме всех сил данной системы, является главным векторомэтой системы:
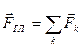 . .
|
Модуль и направление главного вектора можно найти по формулам:
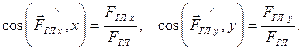 |
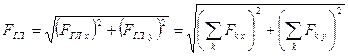 ,
,
Все присоединённые пары 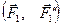 ,
, 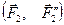 ,
, 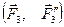 ,
, 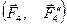 можно сложить по правилу сложения пар (см. п. 1.3.3., Теорема 3.), лежащих в одной плоскости, и, следовательно, заменить их одной, результирующей парой. Моменты этих пар, очевидно, равны моментам данных сил
можно сложить по правилу сложения пар (см. п. 1.3.3., Теорема 3.), лежащих в одной плоскости, и, следовательно, заменить их одной, результирующей парой. Моменты этих пар, очевидно, равны моментам данных сил 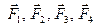 относительно центра приведения О, т.е.
относительно центра приведения О, т.е. 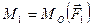 ,
, 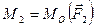 ,
, 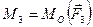 ,
, 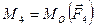 . Отсюда момент результирующей пары вычисляется по формуле
. Отсюда момент результирующей пары вычисляется по формуле
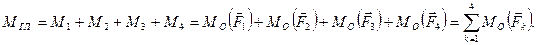
Алгебраическая сумма моментов всех данных сил, расположенных произвольно на плоскости, относительно какой-либо точки О называется главным моментом данной плоской системы сил относительно этой точки:
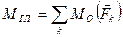 . .
|
Таким образом, всякую плоскую системусил всегда можно заменить одной силой, равной главному вектору системы и приложенной в произвольной точке О, и парой, момент которой равен главному моменту данной системы сил относительно той же точки.
Следует отметить, что сила 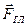 заменят данную систему сил не одна, а вместе с парой, поэтому её нельзя считать равнодействующей.
заменят данную систему сил не одна, а вместе с парой, поэтому её нельзя считать равнодействующей.
Модуль и направление главного вектора не зависят от выбора центра О приведения, так как все силы переносятся параллельно их начальным направлениям, и силовой многоугольник, следовательно, будет во всех случаях одним и тем же. Наоборот, численное значение и знак главного момента зависят, вообще говоря, от выбора центра приведения, так как с изменением центра приведения изменяются моменты данных сил относительно этого центра, а следовательно, и их алгебраическая сумма. Поэтому, когда говорят о главном моменте данной системы сил, то всегда указывают, к какой точке относится этот момент.
1.4.3. Для равновесия произвольной плоской системы сил необходимо и достаточно, чтобы и главный вектор, и главный момент этой системы относительно любой точки плоскости действия сил равнялись нулю:
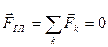 и и 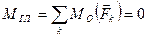 . .
|
1.4.4. Рассмотрим различные формы аналитических условия равновесия.
1)Для равновесия системы сил, как угодно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю как сумма проекций всех сил на каждую из двух любых координатных осей, лежащих в плоскости действия сил, так и сумма алгебраических величин моментов всех сил относительно любой точки той же плоскости:
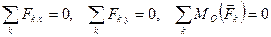 . .
|
2)Для равновесия системы сил, как угодно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю алгебраические суммы моментов всех сил относительно трёх любых, но не лежащих на одной прямой, точек плоскости действия сил:
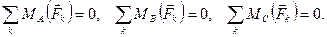
|
3)Для равновесия системы сил, как угодно расположенных на плоскости, необходимо и достаточно, чтобы равнялись нулю алгебраические суммы моментов всех сил относительно двух любых точек плоскости и сумма проекций всех сил на какую-либо одну ось, лежащую в той же плоскости, но не перпендикулярную к прямой, проходящей через выбранные центры моментов:
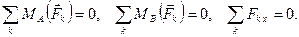
|
Указанные условия равновесия используются для определения реакций опор, с помощью которых закрепляются различные конструкции (шарнирно-подвижная опора, шарнирно-неподвижная опора, жёсткая заделка и т.д.).
Важно заметить, что во всех случаях для произвольной плоской системы сил можно составить только три независимых уравнения равновесия.
При решении задач рекомендуется за центр моментов выбирать точку, лежащую на линии действия одной из неизвестных сил. момент силы относительно таким образом выбранного центра равен нулю (вследствие равенства нулю её плеча), и эта неизвестная сила исключается из уравнения моментов.
Вопросы для самопроверки.
1. Опишите способ приведения произвольной плоской системы сил к данному центру.
2. Что такое главные вектор сил и чему он равен? Зависит ли главный вектор сил от выбора центра приведения?
3. Что такое главные момент сил и чему он равен? Зависит ли главный момент сил от выбора центра приведения?
4. В чём состоят необходимые и достаточные условия равновесия произвольной системы сил на плоскости?
5. Почему в шарнирных опорах брусьев возникают только реактивные силы, а в жёсткой заделке, кроме того, и реактивный момент?
Дата добавления: 2015-09-02; просмотров: 1858;
