Тема 1.6. Центр тяжести тела.

1.6.1.Сложение параллельных сил. Центр параллельных сил.

1.6.2. Понятие о центре тяжести тела.

1.6.3. Координаты центра тяжести тела.

1.6.4. Центр тяжести симметричного тела.

1.6.5. Определение положения центра тяжести фигур и тел сложной формы.

1.6.1. Равнодействующая двух параллельных сил, направленных в одну сторону (рис. 1.6.1.), им параллельна, направлена в ту же сторону и равна по модулю их сумме:

;

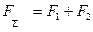линия действия равнодействующей лежит между линиями действия составляющих сил на расстояниях от них, обратно пропорциональных модулям этих сил:

.

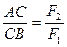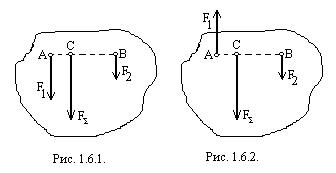Равнодействующая двух не равных по модулю параллельных сил, направленных в противоположные стороны (рис. 1.6.2.), им параллельна, направлена в сторону большей силы и равна по модулю их разности:

;

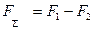линия действия равнодействующей лежит за большей силой на расстояниях от линий действия составляющих сил, обратно пропорциональных модулям этих сил:

.

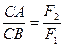Зная правила сложения двух параллельных сил, нетрудно путём последовательного сложения найти равнодействующую и для любой системы параллельных сил 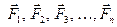. Если силы данной системы направлены в одну сторону, то её равнодействующая, очевидно, параллельна данным силам и направлена в ту же сторону. Модуль равнодействующей равен сумме модулей составляющих сил:

.

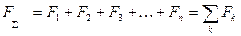Остаётся определить положение точки С, через которую проходит линия действия равнодействующей. За точку приложения равнодействующей. Конечно, может быть взята любая точка, лежащая на линии её действия, но оказывается, что только одна из них, именно точка С, определённая путём последовательного сложения сил, обладает особым, весьма важным свойством: если мы повернём все данные силы вокруг их точек приложения на одинаковый угол, не нарушая их параллельности, то линия действия их равнодействующей, повернувшись на тот же самый угол, будет вновь проходить через точку С.

Точка С носит название центра системы параллельных сил.

Таким образом, центром данной системы параллельных сил называется точка, через которую проходит линия действия их равнодействующей при любом повороте сил системы вокруг их точек приложения на один и тот же угол в одну и ту же сторону.

Воспользовавшись формулами аналитической геометрии, можно получить формулы координат 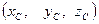центра системы параллельных сил:

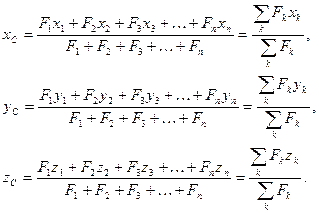
где 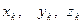- координаты точки приложения силы .

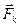В случае, если в систему входят силы противоположного направления, причём 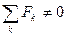, то под 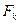надо понимать алгебраическое значение силы, т.е. её модуль, взятый со знаком плюс при направлении силы в одну сторону и со знаком минус при направлении силы в другую сторону.

1.6.2. По закону всемирного тяготения на все частицы тела, находящегося вблизи земной поверхности, действуют силы притяжения их к Земле, т.е. силы тяжести. Эти силы направлены о радиусу Земли и пересекаются приблизительно в её центре; но так как расстояние до центра Земли чрезвычайно велико по сравнению с расстояниями между частицами тела обычных размеров, то с очень большой точностью можно считать силы тяжести всех отдельных частиц тела параллельными.

Равнодействующая сил тяжести всех отдельных частиц тела называется силой тяжести тела.

Как бы мы ни поворачивали тело и не изменяли его положение в пространстве, силы тяжести его отдельных частиц останутся параллельными друг другу (вертикальными). Но при таком повороте равнодействующая параллельных сил всегда проходит через одну и ту же точку – центр данной системы параллельных сил.

Центр тяжести тела есть такая, неизменно связанная с этим телом, точка, через которую проходит линия действия силы тяжести данного тела при любом положении тела в пространстве.

Заметим, что неправильно представлять себе центр тяжести как материальную частицу тела, к которой непосредственно приложена сила тяжести тела. Центр тяжести тела есть всего лишь точка, через которую всегда проходит линия действия силы тяжести тела. Центр тяжести тела может лежать в точке, где вовсе нет материальных частиц, принадлежащих данному телу. Так, например, центром тяжести однородного шара с концентрической полостью служит его геометрический центр.

1.6.3. Так как центр тяжести тела есть центр параллельных сил тяжести его частиц, то его координаты определяются по формулам 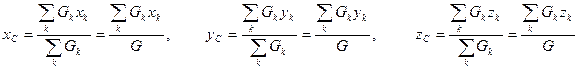, (1.6.1.)

где 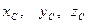- координаты центра тяжести тела, 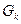- силя тяжести произвольной частицы тела, 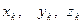- координаты этой частицы, - сила тяжести всего тела.

Рассмотрим частные случаи.

1) Для однородного (одинаковой плотности по всему объёму) тела координаты центра тяжести определяются по формулем

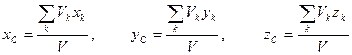, (1.6.2.)

где -объём одной частицы тела.

2) Для однородной тонкой пластины постоянной толщины координаты центра тяжести определяются по формулам

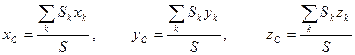, (1.6.3.)

где 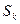-площадь произвольного элемента фигуры.

3) Для однородного тела, площадь поперечного сечения которого одинакова по всей его длине и мала по сравнению с нею , координаты центра тяжести определяются по формулам

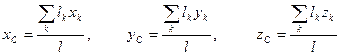, (1.6.4.)

где 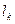- элемент длины тела.

1.6.4. Теорема. Если однородное тело имеет плоскость (ось, центр) симметрии, то центр тяжести его лежит соответственно в плоскости (на оси, в центре) симметрии.

Следствия. 1.Центр тяжести отрезка материальной однородной прямой линии лежит в его середине.

2.Центр тяжести площади однородного параллелограмма лежит в точке пересечения его диагоналей, являющихся центром симметрии параллелограмма.

3.Центры тяжести площадей правильного многоугольника, круга, эллипса и объёма шара лежат в их геометрических центрах.

1.6.5. Аналитический способ.Для определения положения центра тяжести фигур и тел сложной геометрической формы их разбивают на такие части простейшей формы (если, конечно, это возможно), для которых положение центра тяжести известно, а затем определяют положение центра тяжести всей фигуры или тела по соответствующим формулам (см. п. 1.6.3.). Если рассматриваемые фигуры или тела неоднородны, т.е. если они состоят из частей одинаковой плотности, то, разделив их на однородные части, умножают входящие в формулы (1.6.2.) – (1.6.4.) объёмы, площади и длины этих частей на соответствующий каждой части удельный вес. Если в данном теле или фигуре имеются полости или отверстия, то для определения центра тяжести такого тела или фигуры пользуются теми же примами и формулами, считая при этом объёмы и площади вырезанных частей отрицательными.

В технической практике широкое распространение имеет стальной прокат различного профиля. Форма этих поперечных сечений, так же как и их размеры, устанавливаются государственными стандартами. В таблицах так зазываемого нормального сортамента прокатной стали, имеющихся в различного рода технических справочниках, приводятся для каждого калибра соответствующего профиля все необходимые сведения, в частности геометрические размеры профиля, площадь сечения, координаты центра тяжести и пр. Пользуясь этими данными, можно указанными выше приемами определить положение центра тяжести и составного сечения, полученного путём соединения нескольких стандартных профилей.

Экспериментальный способосуществляется двумя методами – подвешивания и взвешивания. Метод подвешивания заключается в том, что плоское тело, которое нельзя разбить на простейшие фигуры с известным положением центра тяжести, подвешивают на нити. Прочерчивают линию вдоль этой нити на плоскости тела. Затем эту плоскую фигуру открепляют и подвешивают за другую точку, после чего вновь проводят вертикальную линию (вдоль линии подвеса). Пересечение этих двух линий даёт точку, в которой находится центр тяжести.

Метод взвешивания обычно применяется для крупных изделий: самолётов,. Вертолётов и других машин. Если известна масса, например, самолёта, то ставят на весы задние колёса и по показанию весов определяют реакцию 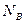. Затем составляют одно из уравнений равновесия; удобнее составить сумму моментов относительно точки А (передние колёса):

,

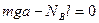где 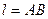, 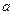- расстояние между передними колёсами и линией действия силы тяжести.

Вопросы для самопроверки.

1. Является ли центр тяжести центром параллельных сил?

2. Перечислите способы определения положения центра тяжести твёрдого тела.

3. Расскажите об аналитическом способе определения положения центра тяжести фигуры.

КИНЕМАТИКА

Тема 1.7. Основные понятия кинематики.

1.7.1. Предмет кинематики.

1.7.2. Траектория. Путь. Перемещение.

1.7.3. Способы задания движения точки.

1.7.4. Скорость точки.

1.7.5. Ускорение точки.

1.7.1. Кинематикой называется раздел теоретической механики, изучающий движение тел лишь с геометрической стороны, вне зависимости от факторов, обуславливающих тот или иной характер этого движения. Кинематика целиком основывается на аксиомах и положениях геометрии, но отличается от неё тем, что кроме пространства, проходимого движущимся телом, она рассматривает ещё и время, за которое совершается движение.

Всякое механическое движение материального тела можно наблюдать и изучать лишь по отношению к каким-либо другим телам. Твёрдое тело, по отношению к которому с помощью системы координат определяется положение других тел в разные моменты времени, называется телом отсчёта. Тело отсчёта, связанные с ним система координат и часы называются системой отсчёта. Пространство в механике рассматривается как трёхмерное евклидово пространство. Все измерения в нём производятся на основании методов евклидовой геометрии. За единицу длины при измерении расстояний принимается один метр.

Время в механике считается универсальным, т.е. протекающим одинаково во всех системах отсчёта. За единицу времени принимается одна секунда. Время является скалярной непрерывно меняющейся величиной. В задачах кинематики его принимают за независимое переменное. Все другие величины (расстояния, скорости и т.д.) рассматриваются как функции времени.

По характеру рассматриваемых материальных объектов кинематику делят на кинематику точки и кинематику абсолютно твёрдого тела. При движении тела все отдельные его точки в общем случае совершают различные движения. Поэтому кинематику начнём изучать с рассмотрения движения точки, т.е. с кинематики точки.

1.7.2. В процессе своего движения точка последовательно занимает различные положения относительно принятой системы отсчета, причем эти положения непрерывно сле­дуют одно за другим.

Геометрическое место положений движущейся точки в рассматриваемой системе отсчета называется траекто­рией этой точки (рис. 1.7.1.).

Движение точки называется прямолинейным, если ее траектория—прямая линия, и криволинейным, если ее траектория—кривая линия. В зависимости от формы кривой криволинейное движение в свою очередь может быть различным: круговым (когда траектория точки — окружность или ее дуга), эллиптическим (когда траекто­рия точки—эллипс), винтовым (когда траектория точки — винтовая линия) и т. д.

Форма траектории зависит, конечно, от выбора си­стемы отсчета. Например, камень, брошенный вертикально вверх с тележки, движущейся поступательно, прямолинейно и равномерно, будет относительно наблюдателя, находящегося на тележке, двигаться прямолинейно, а относительно наблюдателя, стоящего на той поверхности., по которой движется тележка, - по параболе. Всякая классификация движений носит отно­сительный характер и имеет смысл только тогда, когда эти движения рассматриваются относительно одной и той же системы отсчета.

Расстояние, пройденное телом вдоль траекто­рии движения, называют пройденным путем (рис. 1.7.1.). Путь обозначают букво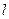й или 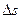. Основной едини­цей пути является 1 метр (м).

Если известны траектория движения тела, его начальное положение и пройденный им путь, то можно определить положение тела в тот или иной момент времени. Если траектория не известна, то положение тела, зная пройденный им путь, определить нельзя, так как этот путь мог быть пройден те­лом в любом направлении. В этом случае надо знать направление движения тела и расстояние, пройденное в этом направлении.

Пусть в начальный момент времени тело за­нимало положение А, а в момент време­ни t положение В (рис. 1.7.1.). Направление от А к В и есть направление движения тела.

Перемещениемтела называют направлен­ный отрезок прямой (вектор), соединяющий начальное положение тела с его конечным по­ложением.Вданном случае — это вектор 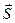(рис. 1.7.1.).

Перемещение — величина векторная. Она имеет определенное числовое значение и направ­ление. Перемещение – величина относительная.

Следует иметь в виду, что перемещение тела может не совпадать с траекторией, а модуль пе­ремещения с пройденным путем. Например, по­езд отправился из Москвы в Санкт-Петербург и вернулся обратно. Расстояние между этими го­родами 650 км. Перемещение поезда в данном случае равно нулю, а его путь — 1300 км.

Если точка в равные, произвольно взятые, промежут­ки времени проходит пути одинаковой длины, то дви­жение точки называется равномерным, в противном слу­чае движение точки называется неравномерным или пере­менным.

Движение точки характеризуется признаками, уста­навливаемыми каждой из двух данных выше классифи­каций. Как прямолинейное, так и криволинейное движение точки может одновременно быть или равномерным, или неравномерным (переменным) движением.

1.7.3. Движение тела считается известным тогда, когда мы имеем возможность определить его положение относительно выбранной системы отсчёта в каждый момент.Рассмотрим два способа задания движения точки: естественный и координатный.

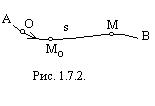Естественный способ задания движения точки. Задать движение точки естественным способом – это значит: а) задать траекторию АВ движения точки в некоторой системе отсчёта Oxyz; б) на траектории выбрать начало отсчёта О и положительное направление отсчёта расстояний; в) указать закон движения точки М по данной траектории в виде уравнения 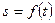, где s – расстояние точки М, измеряемое по дуге ОМ, от начала отсчёта в данный момент времени t (рис. 1.7.2.).

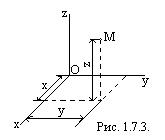Координатный способ задания движения. Положение точки в пространстве трёх измерений можно однозначно определить, задав три её координаты в некоторой системе отсчёта (рис. 1.7.3.).

В качестве системы отсчёта в дальнейшем используется прямоугольная декартова система координат Oxyz, которая условно принимается за неподвижную. Задать движение точки в координатной форме – это значит задать координаты этой точки как функции времени:

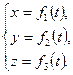(1.7.1.)

Уравнения (1.7.1.) называются уравнениями движения точки. Уравнения движения (1.7.1.) точки в прямоугольных координатах , определяя положение движущейся точки в любой момент времени, определяют тем самым и её траекторию.

1.7.4. Скоростью точки называется вектор, определяющий в каждый данный момент быстроту и направление движения точки.

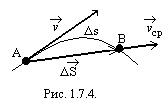Пусть материальная точка движется по какой-либо криволинейной траектории (рис. 1.7.4.) так, что в течении малого промежутка времени 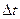точка пройдёт путь 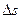и получит элементарное (бесконечно малое) перемещение 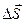. Вектором средней скорости 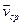называется отношение перемещения 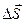точки к промежутку времени :

.

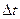Направление вектора средней скорости совпадает с направлением вектора 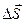. При неограниченном уменьшении 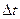средняя скорость стремится к предельному значению, которое называется мгновенной скоростью :

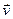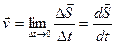. (1.7.2.)

Мгновенная скорость 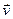, таким образом, есть векторная величина, равная первой производной вектора перемещения движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости 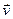направлен по касательной к траектории в сторону движения. По мере уменьшения 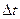путь 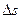всё больше будет приближаться к 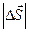, поэтому модуль мгновенной скорости

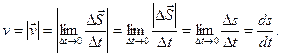(1.7.3.)

Таким образом, модуль мгновенной скорости 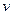равен первой производной пути по времени.

При неравномерном движении модуль мгновенной скорости с течением времени изменяется.

1.7.5. В случае неравномерного движения важно знать, как быстро изменяется скорость с течением времени. Физическая величина, характеризующая быстроту изменения скорости по модулю и направлению, называется ускорением.

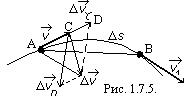
Рассмотрим плоское движение , т.е. движение, при котором все участки траектории точки лежат в одной плоскости. Пусть вектор 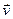задаёт скорость точки А в момент времени 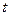. За промежуток времени 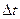движущаяся точка перешла в положение В и приобрела скорость, отличную от 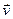как по модулю, так и по направлению и равную 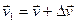(рис. 1.7.5.). Перенесём вектор 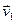в точку А и найдём .

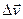Средним ускорением 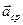нераномерного движения в интервале от 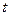до 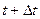называется векторная величина, равная отношению изменения скорости 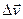к интервалу времени :

.

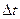Мгновенным ускорением 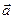материальнойточки в момент времени 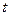будет предел среднего ускорения:

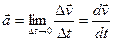. (1.7.4.)

Таким образом, ускорение 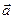есть векторная величина, равная первой производной скорости по времени.

Разложим вектор 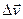на две составляющие. Для этого из точки А (рис. 1.7.5.) по направлению скорости 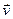отложим вектор 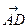, по модулю равный 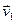. Очевидно, что вектор 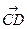, равный 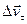, определяет изменение скорости за время 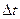по модулю: 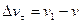. Вторая же составляющая 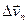вектора 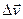характеризует изменение скорости за время 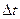по напрвлению.