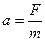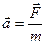Тема 1.11. Сложное движение твёрдого тела.
1.11.1.Ппонятие сложного движения тела.
1.11.2. Понятие плоскопараллельного движения тела.
1.11.3.Разложение движения плоской фигуры на поступательное и вращательное .
1.11.4. Скорость точки плоской фигуры.
1.11.5. Мгновенный центр скоростей фигуры.
1.11.6. Сложение вращений вокруг параллельных осей.
1.11.7. Планетарные и дифференциальные передачи
1.11.1.Понятие сложного движения тела аналогично понятию сложного движения точки. В ряде случаев движение тела относительно неподвижной системы отсчета удобно рассматривать как движение сложное, состоящее из двух движений: относительного, т. е. движения тела по отношению к некоторой подвижной системе отсчета, и переносного—движения тела вместе с подвижной системой отсчета по отношению к неподвижной.
Всякое сложное движение тела можно свести к той или иной совокупности поступательных и вращательных движений, являющихся не только простейшими, но и основными видами движения твердого тела. Задача определения абсолютного движения тела сводится обычно поэтому к задаче сложения или поступательных движений, или вращательных движений, или вращательного и поступательного движений, в зависимости от того, какими движениями будут переносное и относительное движения тела. Некоторые, особо важные для практики, частные случаи такого сложения движений тела и рассматриваются в данной теме, например способы определения абсолютных скоростей его точек в данный момент времени.
1.11.2.Плоскопараллельным или плоским движением твердого тела называется такое движение твердого тела, при котором все его точки движутся в плоскостях, параллельных некоторой неподвижной плоскости.
Частным случаем такого движения является уже изученное нами вращение твердого тела вокруг неподвижной оси. При вращательном движении, как мы знаем, все точки тела движутся в плоскостях, перпендикулярных к оси вращения, и, следовательно, любая из этих плоскостей может быть принята за неподвижную, параллельно которой движутся все точки тела. В ряде случаев плоскопараллельное движение тела может быть одновременно и поступательным движением. Однако поступательное движение нельзя, вообще говоря, рассматривать как частный случай плоскопараллельного движения. Не всякое поступательное движение тела есть плоскопараллельное движение, так же как и не всякое плоскопараллельное движение тела есть поступательное движение.
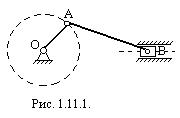 Плоскопараллельное движение имеет огромное распространение в технике. Подавляющее большинство встречающихся на практике механизмов являются плоскими, т. е. представляют собой сочленение твердых тел, совершающих плоскопараллельное движение. Таково, например, движение всех звеньев кривошипно-ползунного механизма (рис. 1.11.1) , состоящего из кривошипа ОА, ползуна В и шарнирно соединенного с ними шатуна АВ. Все точки каждого из звеньев движутся параллельно некоторой неподвижной плоскости (плоскости чертежа на рис. 1.11.1). Плоскопараллельное движение кривошипа является вместе с тем и вращательным движением вокруг неподвижной оси О. Плоскопараллельное движение ползуна одновременно и поступательное движение вдоль неподвижных направляющих. Плоскопараллельное же движение шатуна не будет ни вращательным (так как шатун не имеет неподвижных точек), ни поступательным (так как прямая АВ не остается при движении шатуна параллельной самой себе).
Плоскопараллельное движение имеет огромное распространение в технике. Подавляющее большинство встречающихся на практике механизмов являются плоскими, т. е. представляют собой сочленение твердых тел, совершающих плоскопараллельное движение. Таково, например, движение всех звеньев кривошипно-ползунного механизма (рис. 1.11.1) , состоящего из кривошипа ОА, ползуна В и шарнирно соединенного с ними шатуна АВ. Все точки каждого из звеньев движутся параллельно некоторой неподвижной плоскости (плоскости чертежа на рис. 1.11.1). Плоскопараллельное движение кривошипа является вместе с тем и вращательным движением вокруг неподвижной оси О. Плоскопараллельное движение ползуна одновременно и поступательное движение вдоль неподвижных направляющих. Плоскопараллельное же движение шатуна не будет ни вращательным (так как шатун не имеет неподвижных точек), ни поступательным (так как прямая АВ не остается при движении шатуна параллельной самой себе).
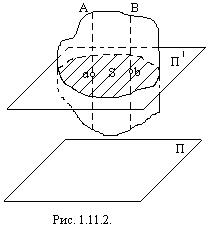 Выясним теперь, как можно упростить изучение этого весьма важного вида движения твердого тела. Пусть тело движется параллельно некоторой неподвижной плоскости П (рис. 1.11.2). Если мы пересечем данное тело плоскостью П', параллельной неподвижной плоскости П, то в сечении получится какая-то плоская фигура S. Эта фигура будет перемещаться при движении тела, оставаясь вcё время в той же плоскости П'. Очевидно, что при таком движении тела все его точки, лежащие на перпендикуляре Аа к плоскости фигуры S, восставленном в какой-нибудь ее точке а, движутся совершенно одинаково, так же, как и точка а этой фигуры. Все точки тела, лежащие на перпендикуляре Вb, движутся так же, как и точка b фигуры S, и т. д.
Выясним теперь, как можно упростить изучение этого весьма важного вида движения твердого тела. Пусть тело движется параллельно некоторой неподвижной плоскости П (рис. 1.11.2). Если мы пересечем данное тело плоскостью П', параллельной неподвижной плоскости П, то в сечении получится какая-то плоская фигура S. Эта фигура будет перемещаться при движении тела, оставаясь вcё время в той же плоскости П'. Очевидно, что при таком движении тела все его точки, лежащие на перпендикуляре Аа к плоскости фигуры S, восставленном в какой-нибудь ее точке а, движутся совершенно одинаково, так же, как и точка а этой фигуры. Все точки тела, лежащие на перпендикуляре Вb, движутся так же, как и точка b фигуры S, и т. д.
Отсюда следует, что для определения плоскопараллельного движения тела достаточно знать движение неизменяемой плоской фигуры, получающейся при пересечении тела какой-либо плоскостью, параллельной данной неподвижной плоскости.
Изучением движения этой плоской фигуры в ее плоскости можно заменить, следовательно, изучение плоскопараллельного движения тела.
 Заметим также, что положение на плоскости неизменяемой плоской фигуры вполне определяется положением двух любых ее точек или, что все равно, положением какого-либо, прямолинейного отрезка, неизменно связанного с движущейся фигурой. Допустим, что при перемещении этой фигуры неизменно связанный с нею отрезок
Заметим также, что положение на плоскости неизменяемой плоской фигуры вполне определяется положением двух любых ее точек или, что все равно, положением какого-либо, прямолинейного отрезка, неизменно связанного с движущейся фигурой. Допустим, что при перемещении этой фигуры неизменно связанный с нею отрезок 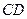 занял в той же плоскости положение
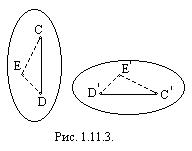
занял в той же плоскости положение 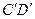 (рис. 1.11.3.). Так как расстояние DEи Слюбой точки Eфигуры от данных ее точек Dи С неизменны, то новое положение этой точки легко определяется построением треугольника
(рис. 1.11.3.). Так как расстояние DEи Слюбой точки Eфигуры от данных ее точек Dи С неизменны, то новое положение этой точки легко определяется построением треугольника 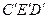 , равного
, равного 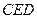 .
.
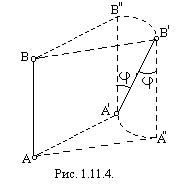 1.11.3. Пусть неизменно связанная с плоской фигурой произвольная прямая перемещается при движении этой фигуры за некоторый промежуток времени из положения АВ в положение А'В' (рис. 1.11.4.).
1.11.3. Пусть неизменно связанная с плоской фигурой произвольная прямая перемещается при движении этой фигуры за некоторый промежуток времени из положения АВ в положение А'В' (рис. 1.11.4.).
Это перемещение плоской фигуры можно представить себе составленным из поступательного и вращательного перемещений (рис. 1.11.4.). В самом деле, перемещение прямой АВ в положение А'В' можно было бы получить поступательным ее перемещением в положение А'В" или А"В' и вращательным перемещением этой прямой вокруг оси, проходящей соответственно через точку А' или точку В' и перпендикулярной к плоскости фигуры.
Произвольная точка, связанная с движущейся фигурой и принимаемая за центр ее поворота, называется полюсом. Нетрудно доказать, что, выбирая различные полюсы, мы изменяем только поступательную часть перемещения фигуры, угол же поворота и направление вращения фигуры от выбора полюса не зависят.
Таким образом, мы приходим к выводу: всякое движение плоской фигуры в ее плоскости можно разложить на два движения: 1) поступательное движение вместе с произвольно выбранной точкой фигуры (полюсом) и 2) вращательное движение вокруг этой точки.
Так как угол 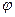 поворота фигуры и направление ее вращения не зависят от выбора полюса, то и угловая скорость
поворота фигуры и направление ее вращения не зависят от выбора полюса, то и угловая скорость 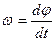 плоской фигуры от выбора полюса не зависит.
плоской фигуры от выбора полюса не зависит.
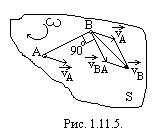 1.11.4. Пусть плоская фигура S движется в своей плоскости (рис. 1.11.5.). примем какую-либо произвольную точку А фигуры S за полюс. Тогда можно считать, что по отношению к неподвижной системе отсчёта (связанной с плоскостью, в которой движется фигура) любая другая точка В фигуры участвует одновременно в двух движениях: переносном- вместе с фигурой в её поступательном движении со скоростью
1.11.4. Пусть плоская фигура S движется в своей плоскости (рис. 1.11.5.). примем какую-либо произвольную точку А фигуры S за полюс. Тогда можно считать, что по отношению к неподвижной системе отсчёта (связанной с плоскостью, в которой движется фигура) любая другая точка В фигуры участвует одновременно в двух движениях: переносном- вместе с фигурой в её поступательном движении со скоростью 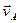 выбранного полюса и оросительном движении вокруг полюса А.Тогда скорость (абсолютная скорость)
выбранного полюса и оросительном движении вокруг полюса А.Тогда скорость (абсолютная скорость) 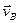 любой точки B плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости
любой точки B плоской фигуры в каждый данный момент равна геометрической сумме двух скоростей: скорости 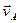 другой, произвольно выбранной, точки A фигуры (полюса) и вращательной скорости
другой, произвольно выбранной, точки A фигуры (полюса) и вращательной скорости 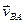 первой точки B относительно второй точки A:
первой точки B относительно второй точки A:
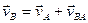 .
.
Определив вращательную скорость 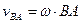 точки В относительно полюса и зная скорость
точки В относительно полюса и зная скорость 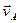 самого полюса, находим искомую скорость точки В как диагональ параллелограмма, построенного на векторах
самого полюса, находим искомую скорость точки В как диагональ параллелограмма, построенного на векторах 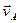 и
и 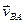 оставляющих скоростей (рис. 1.11.5.).
оставляющих скоростей (рис. 1.11.5.).
Обычно за полюс принимается та точка фигуры, скорость которой в данный момент нам известна.
1.11.5. Можно доказать, что при всяком движении плоской фигуры (кроме поступательного) всегда можно отыскать такую точку, лежащую или на самой движущейся фигуре, или на ее мысленном продолжении, скорость которой в данный момент равна нулю.
Неизменно связанная с движущейся плоской фигурой точка Р, скорость которой в данный момент времени равна нулю, называется мгновенным центром скоростей этой фигуры. Мгновенный центр Р скоростей фигуры всегда лежит на линии, проведенной из какой-либо точки фигуры перпендикулярно к направлению скорости этой точки. Если известны направления скоростей двух каких-либо точек фигуры, то мгновенный центр Р скоростей этой фигуры легко находится как точка пересечения линий, проведенных из данных точек фигуры перпендикулярно к векторам скоростей этих точек (рис. 1.11.6.).
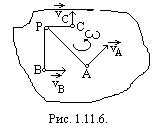 Принимая мгновенный центр Р скоростей фигуры за полюс, легко найти скорости всех остальных точек фигуры в этот момент времени:
Принимая мгновенный центр Р скоростей фигуры за полюс, легко найти скорости всех остальных точек фигуры в этот момент времени: 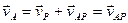 . Следовательно, скорость любой точки плоской фигуры равна вращательной скорости этой точки вокруг мгновенного центра скоростей фигуры. Тогда
. Следовательно, скорость любой точки плоской фигуры равна вращательной скорости этой точки вокруг мгновенного центра скоростей фигуры. Тогда 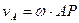 , т.е. модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от соответствующего данному моменту мгновенного центра скоростей фигуры. Направлены же скорости различных точек фигуры перпендикулярно к отрезкам, соединяющим соответствующие точки с мгновенным центром скоростей, в сторону вращения фигуры (рис. 1.11.6.). Таким образом, скорости различных точек плоской фигуры в каждый данный момент времени распределяются так, как если бы фигура вращалась в этот момент времени вокруг мгновенного центра скоростей, занимающего в разные моменты различные положения как относительно движущейся фигуры, так и относительно неподвижной плоскости, в которой движется фигура.
, т.е. модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от соответствующего данному моменту мгновенного центра скоростей фигуры. Направлены же скорости различных точек фигуры перпендикулярно к отрезкам, соединяющим соответствующие точки с мгновенным центром скоростей, в сторону вращения фигуры (рис. 1.11.6.). Таким образом, скорости различных точек плоской фигуры в каждый данный момент времени распределяются так, как если бы фигура вращалась в этот момент времени вокруг мгновенного центра скоростей, занимающего в разные моменты различные положения как относительно движущейся фигуры, так и относительно неподвижной плоскости, в которой движется фигура.
Найдя положение мгновенного центра скоростей Р и зная для данного момента скорость 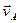 какой-либо точки А фигуры не только по направлению, но и по модулю, легко найти и угловую скорость фигуры, соответствующую этому моменту времени. Угловая скорость фигуры в каждый момент равна отношению модуля соответствующей этому моменту скорости какой-либо точки фигуры к расстоянию от этой точки до мгновенного центра скоростей:
какой-либо точки А фигуры не только по направлению, но и по модулю, легко найти и угловую скорость фигуры, соответствующую этому моменту времени. Угловая скорость фигуры в каждый момент равна отношению модуля соответствующей этому моменту скорости какой-либо точки фигуры к расстоянию от этой точки до мгновенного центра скоростей:
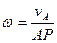
Направление же вращения фигуры определяется известным направлением скорости ее точки.
Указанный выше прием определения мгновенного центра скоростей фигуры как точки пересечения перпендикуляров, восставленных к векторам скоростей двух точек фигуры, неприменим, очевидно, в тех случаях, когда эти скорости параллельны. При этом возможны два случая.
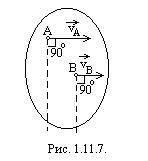 1. Скорости двух точек А и В фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.7.).
1. Скорости двух точек А и В фигуры параллельны, но эти точки не лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.7.).
Расстояния данных точек от мгновенного центра скоростей 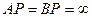 . Угловая скорость фигуры в данный момент
. Угловая скорость фигуры в данный момент 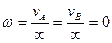 , и вращение фигуры в этот момент, следовательно, отсутствует. А так как всякое абсолютное плоское движение фигуры можно рассматривать как совокупность поступательного движения со скоростью произвольно выбранного полюса и вращательного движения вокруг этого полюса (с угловой скоростью
, и вращение фигуры в этот момент, следовательно, отсутствует. А так как всякое абсолютное плоское движение фигуры можно рассматривать как совокупность поступательного движения со скоростью произвольно выбранного полюса и вращательного движения вокруг этого полюса (с угловой скоростью 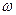 , независящий от выбора полюса), то абсолютные скорости точек фигуры в данном случае равны только скорости полюса. Другими словами, в этом случае фигура совершает в данный момент поступательное движение, и скорости всех её точек в этот момент равны между собой.
, независящий от выбора полюса), то абсолютные скорости точек фигуры в данном случае равны только скорости полюса. Другими словами, в этом случае фигура совершает в данный момент поступательное движение, и скорости всех её точек в этот момент равны между собой.
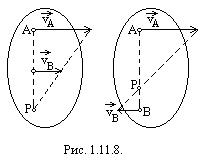 2. Скорости двух точек А и В фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.8.).
2. Скорости двух точек А и В фигуры параллельны, и эти точки лежат на одном перпендикуляре к направлению данных скоростей (рис. 1.11.8.).
Так как мгновенный центр скоростей всегда лежит на перпендикуляре, восставленном в любой точке фигуры к направлению ее скорости, а модули скоростей различных точек фигуры в каждый данный момент пропорциональны расстояниям этих точек от мгновенного центра, то положение этой точки Р на перпендикуляре может быть найдено из пропорции 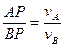 (рис. 1.11.8.).
(рис. 1.11.8.).
Если при этом 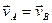 то фигура совершает в данный момент поступательное движение (так же как и в предыдущем случае).
то фигура совершает в данный момент поступательное движение (так же как и в предыдущем случае).
В практических задачах часто приходится иметь дело со случаями, когда плоская фигура движется так, что ее контур катится без скольжения по некоторой неподвижной кривой. Так как в каждый данный момент у движущейся плоской фигуры может быть только одна точка, имеющая скорость, равную нулю, а при качении без скольжения таковой является точка фигуры, в которой она касается неподвижной кривой, то при качении скольжения контура фигуры по неподвижной кривой мгновенным центром скоростей будет точка касания этого контура с неподвижной кривой.
1.11.6. Абсолютное движение тела., участвующего в двух вращениях вокруг параллельных осей, есть частный случай плоскопараллельного движения тела, и для его определения достаточно рассмотреть движение плоской фигуры S (рис. 1.11.9.), являющейся сечением тела плоскостью, перпендикулярной к данным осям.
Движение же плоской фигуры в ее плоскости можно, как известно, рассматривать в каждый данный момент как вращательное движение этой фигуры вокруг соответствующего этому моменту мгновенного центра в некоторой абсолютной угловой скоростью со. При определении положения мгновенного центра скоростей фигуры и ее абсолютной угловой скорости могут быть три случая, каждый из которых мы и рассмотрим.
I случай. Оба вращения направлены в одну сторону (рис. 1.11.9. ). Обозначим следы осей 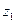 и
и 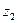 в плоскости фигуры S точками
в плоскости фигуры S точками 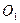 и
и 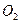 .
.
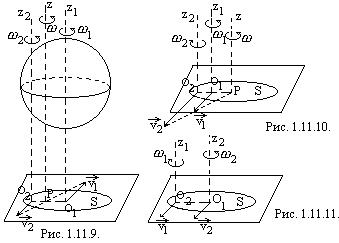 |
· Два вращения, происходящих вокруг параллельных осей в одну сторону, можно в каждый данный момент заменить одним вращением, происходящим в ту же сторону вокруг мгновенной оси, параллельной данным осям, лежащей в одной плоскости с ними и делящей расстояние между ними на части, обратно пропорциональные угловым скоростям составляющих вращений:
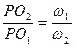 .
.
· Абсолютная угловая скорость тела равна сумме угловых скоростей составляющих вращений:
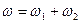 .
.
II случай. Оба вращения направлены в разные стороны с различной угловой скоростью (рис. 1.11.10.).
· Два вращения, происходящие вокруг параллельных осей в разные стороны с различными угловыми скоростями, можно заменить в каждый данный момент одним вращением, происходящим вокруг мгновенной оси, параллельной данным, в сторону вращения с большей угловой скоростью. Мгновенная ось сложного вращения лежит в одной плоскости с данными осями за осью с большей угловой скоростью и отстоит от данных осей на расстояниях, обратно пропорциональных угловым скоростям составляющих вращений:
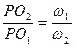 .
.
· Абсолютная угловая скорость тела равна разности угловых скоростей составляющих вращений:
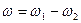 .
.
III случай. Оба вращения направлены в разные стороны, а их угловые скорости равны по численному значению (рис. 1.1.11.).
· Два вращения тела, происходящие вокруг параллельных осей в разные стороны с равными угловыми скоростями, можно заменить в данный момент одним поступательным его движением, происходящим в направлении, перпендикулярном к плоскости, проведенной через оси составляющих вращений.
· Модуль скорости поступательного движения тела равен при этом в данный момент произведению угловой скорости 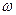 одного из вращений на кратчайшее расстояние
одного из вращений на кратчайшее расстояние 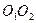 между осями составляющих вращений:
между осями составляющих вращений:
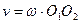 .
.
1.11.7. 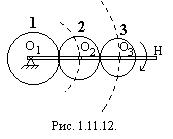 Планетарными и дифференциальными передачами называются механизмы, в которых имеются колеса с подвижными осями, вращающимися вместе с так называемым водилом (Н на рис. 1.11.12.) вокруг неподвижной оси.
Планетарными и дифференциальными передачами называются механизмы, в которых имеются колеса с подвижными осями, вращающимися вместе с так называемым водилом (Н на рис. 1.11.12.) вокруг неподвижной оси.
Колеса, геометрические оси которых неподвижны, называются центральными.
Колеса с подвижными геометрическими осями называются сателлитами.
Колеса с подвижными осями (2 и 3 на, рис. 1.11.12.) совершают сложное движение, вращаясь одновременно вокруг своих осей ( 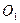 и
и 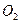 ), закрепленных на водиле, и вместе с водилом вокруг его неподвижной оси
), закрепленных на водиле, и вместе с водилом вокруг его неподвижной оси 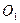 . Движение этих колес подобно движению планет Солнечной системы, почему они и получили название сателлитов (спутников), а сам механизм—название планетарного механизма. По тем же соображениям центральное колесо называют иногда солнечным.
. Движение этих колес подобно движению планет Солнечной системы, почему они и получили название сателлитов (спутников), а сам механизм—название планетарного механизма. По тем же соображениям центральное колесо называют иногда солнечным.
Планетарные механизмы, в которых одно из центральных колес неподвижно, называются простыми планетарными передачами или, чаще, просто планетарными передачами. В отличие от простых планетарных передач, планетарные механизмы, в которых нет неподвижных колес, называются дифференциальными передачами или просто дифференциалами. В дифференциальных передачах одно из центральных колес получает вращение вокруг своей неподвижной оси независимо от вращения водила, т. е. получает его от другого источника.
Планетарные и дифференциальные механизмы имеют широкое распространение в технике, так как позволяют осуществить большие передаточные отношения при малом числе колес и (в дифференциальных механизмах) сложение двух независимых друг от друга угловых скоростей.
Вопросы для самопроверки.
1. Дайте определение плоскопараллельного движения.
2. Расскажите о подходе к изучению плоскопараллельного движения.
3. Сформулируйте теорему о представлении движения плоской фигуры поступательным перемещением и поворотом.
4. Как выражается скорость произвольной точки плоской фигуры через скорость полюса и скорость вращения вокруг полюса?
5. Дайте определение мгновенного центра скоростей.
6. Расскажите об основных приёмах нахождения мгновенного центра скоростей.
7. Расскажите о сложении вращений вокруг параллельных осей.
Тема 1.12. Основные понятия и законы динамики.
1.12.1. Предмет динамики и её две основные задачи.
1.12.2.Основные законы динамики.
1.12.1. Динамикой называется раздел теоретической механики, изучающий зависимость между механическим движением тел и действующими на них силами. Всякое механическое движение тела рассматривается в динамике в связи с физическими факторами, определяющими характер этого движения. В этом отличие динамики от кинематики, где движение рассматривается только с геометрической стороны.
Изучение динамики начинается обычно с изучения движения наиболее простого объекта—материальной точки. Материальной точкой называется такое материальное тело, размерами которого можно пренебречь в условиях данной задачи.
В тех же случаях, когда размерами движущегося (не поступательно) тела пренебречь нельзя, мы можем мысленно разделить его на отдельные, малые сравнительно с расстояниями, играющими роль в данной задаче, части и принять их за материальные точки. Следовательно, всякое тело и любую комбинацию связанных между собой тел можно рассматривать как совокупность материальных точек. Мысленно выделенная совокупность взаимодействующих между собой материальных точек называется механической системой материальных точек или просто системой. Абсолютно твердое тело можно также рассматриватькак систему материальных точек, расстояния между которыми не изменяются ни при каких условиях, т. е. как неизменяемую систему.
Множество частных задач динамики можно свести к двум основным задачам.
· Первая задача динамики. Известно движение данной материальной точки или данной системы. Требуется определить силы, действующие на эту точку или эту систему.
· Вторая задача динамики (обратная первой). Известны силы, действующие на данную материальную точку или данную систему. Требуется определить движение этой точки или этой системы.
Количественные соотношения между различными физическими величинами, связанными с механическим движением материальных тел, устанавливаются в динамике путем математических выводов из основных законов классической механики. Эти законы служат фундаментом, на котором строится все содержание динамики, и потому с них мы и начнем изучение основ динамики.
1.12.1. Первый закон (закон инерции). Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействия со стороны других тел не заставят его изменить это состояние.
Система отсчета, по отношению к которой выполняется закон инерции, называется основной или инерциальной системой, а движение, наблюдаемое по отношению к этой системе, называется абсолютным.
Первый закон динамики указывает на одно из важнейших свойств материи – инертность. По этому закону точка, находящаяся в покое, не может сама сдвинуться с места, а точка, совершающая равномерное и прямолинейное движение, - остановиться или изменить направление и модуль скорости. Для изменения вектора скорости точки необходимо воздействие на неё каких – либо сил.
Любая система отсчета, совершающая относительно инерциальной системы поступательное, прямолинейное и равномерное движение, будет также инерциальной системой. Всякая же система отсчета, движущаяся относительно инерциальной непрямолинейно или хотя бы и прямолинейно, но неравномерно, уже не будет инерциальной системой.
Так как Земля движется вокруг Солнца по некоторой криволинейной орбите, вращаясь при этом вокруг своей оси, то, строго говоря, система отсчета, связанная с Землей, не является инерциальной системой. Однако, вследствие малой кривизны земной орбиты и малой угловой скорости вращения Земли вокруг ее оси (один оборот за сутки), в подавляющем большинстве задач динамики, с которыми приходится иметь дело в обычной технической практике, можно с вполне достаточной точностью считать инерциальной систему отсчета, неподвижную относительно Земли. Поправки приходится при этом вводить лишь в тех сравнительно редких случаях, когда вращением Земли пренебрегать нельзя: в задачах артиллерии и ракет дальнего действия, при изучении морских и воздушных течений и некоторых других, очень быстрых или длящихся очень долго, движений.
Второй закон (основной закон динамики). Ускорение, сообщаемое материальной точке приложенной к ней силой, пропорционально модулю этой силы и совпадает с ней по направлению.
Требуется подчеркнуть, что с направлением силы всегда совпадает направление ускорения, а не направление самого движения (направление скорости). Направление движения может и не совпадать с направлением приложенной к точке силы. Так, точка, брошенная в пустоте под углом к горизонту, движется при полете по кривой линии (параболе), все время изменяя направление своего движения, тогда как действующая на точку сила тяжести (и сообщаемое ею ускорение) всегда направлена по вертикали вниз.
Из повседневного опыта известно, что одна и та же сила сообщает различным телам (даже если они одинаковы по форме и размерам, но различны по своему веществу) неодинаковые ускорения. Модули ускорений, приобретаемых различными телами, зависят, таким образом, не только от модулей действующих на них сил, но и от некоторого свойства самих тел. Это свойство тел характеризуется особой физической величиной, называемой массой.
Масса тела равна отношению его силы тяжести 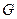 к ускорению
к ускорению 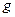 (см. п. 1.8.2.) его свободного падения:
(см. п. 1.8.2.) его свободного падения:
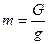 . (1.12.1.)
. (1.12.1.)
Так как ускорение свободного падения не зависит от размеров тела, то масса материальной точки определяется по силе тяжести той же зависимостью (1.12.1.), что и масса любого тела.
Пусть на свободную материальную точку, сила тяжести которой равна G, подействовала сила F, сообщившая ей ускорение а. Согласно рассматриваемому закону модули ускорений, сообщаемых точке приложенными к ней силами, должны быть пропорциональны модулям этих сил. Следовательно,
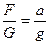 .
.
Отсюда имеем
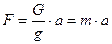 . (1.12.2.)
. (1.12.2.)
Из этого равенства следует, что
|
, (1.12.3.)
т. е. чем больше масса данной точки, тем меньше ускорение точки, сообщаемое ей данной силой. Следовательно, чем больше масса точки, тем медленнее под действием приложенной к ней силы изменяется скорость точки, тем меньше отклоняется ее движение от инерциального. Таким образом, различные материальные точки обладают различной инертностью, и мерой инертности материальной точки является ее масса.
Так как различные точки твердого тела могут совершать различные движения и иметь различные ускорения, то масса тела не во всех случаях является мерой его инерции. Последняя зависит, вообще говоря, не только от значения масс частиц тела, но и от распределения их в теле. Масса тела полностью характеризует его инерцию только в том случае, когда тело совершает поступательное движение (т. е. когда ускорения всех точек тела одинаковы).
В Международной системе единиц (СИ) за единицу массы принят 1 кг, т. е. масса международного прототипа килограмма, а сила, как известно, выражается в ньютонах. Из формулы (1.12.2.) следует, что 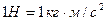 . Таким образом, ньютон—это сила, сообщающая массе в 1 кг ускорение 1 м/с2.
. Таким образом, ньютон—это сила, сообщающая массе в 1 кг ускорение 1 м/с2.
Так как направление силы всегда совпадает с направлением ускорения, сообщаемого ею свободной материальной точке, а масса точки есть скалярная положительная величина, то равенству (1.12.3.) можно придать форму векторного уравнения:
|
. (1.12.4.)
Уравнение (1.12.4.), устанавливающее зависимость между движением материальной точки и действующей на нее силой и являющееся полной математической формулировкой основного закона динамики, называется основным уравнением динамики точки.
С изменением системы отсчета наблюдаемый характер движения точки, а следовательно, и ее ускорение могут изменяться, потому второй закон динамики, так же как и ее первый закон, нельзя применять безотносительно к системе отсчета.
Под ускорением точки, входящим в основное уравнение динамики, надо понимать абсолютное ускорение точки, т. е. ее ускорение относительно системы отсчета, принимаемой за инерциальную.
Третий закон (закон равенства действия и противодействия). Силы, с которыми действуют друг на друга две материальные точки, всегда равны по модулю и направлены по одной прямой (соединяющей данные точки) в противоположные стороны.
Если материальная точка А действует на материальную точку В с силой 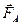 , то точка В действует на точку А с силой
, то точка В действует на точку А с силой 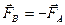 . Пусть масса точки А равна
. Пусть масса точки А равна 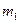 , и ускорение, сообщаемое ей силой
, и ускорение, сообщаемое ей силой 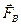 , равно
, равно 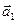 , масса же точки В равна
, масса же точки В равна 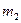 и ускорение, сообщаемое ей силой FA, равно
и ускорение, сообщаемое ей силой FA, равно 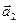 . По основному уравнению динамики
. По основному уравнению динамики 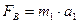 и
и 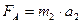 . Согласно же данному закону
. Согласно же данному закону 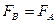 . Отсюда имеем
. Отсюда имеем
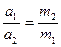 .
.
Модули ускорений, сообщаемых друг другу двумя материальными точками, обратно пропорциональны массам этих точек. Направлены же эти ускорения так же, как и силы взаимодействия, т. е. по одной прямой АВ в противоположные стороны.
Четвертый закон (закон независимости действия сил). Ускорение, получаемое материальной точкой при одновременном действии на нее нескольких сил, равно геометрической сумме тех ускорений, которые получила бы эта точка под действием каждой из данных сил в отдельности.
Пусть на точку, масса которой равна т, одновременно действуют силы 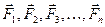 , сообщая ей при этом ускорение
, сообщая ей при этом ускорение 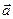 .
.
Ускорения, которые получила бы эта точка при раздельном действии на нее каждой из данных сил, обозначим через 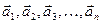 Согласно данному закону, установленному на основании многочисленных опытов Галилеем, будем иметь
Согласно данному закону, установленному на основании многочисленных опытов Галилеем, будем иметь
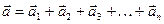 .
.
Если мы умножим обе части данного равенства на скалярный множитель т (на массу точки), то получим 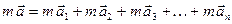 или
или
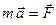 ,
,
где 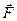 - равнодействующая системы сил
- равнодействующая системы сил 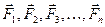 , приложенных к данной точке.
, приложенных к данной точке.
Следовательно, основное уравнение динамики остается в силе и в том случае, когда на точку одновременно действует несколько сил. Под приложенной к точке силой F нужно понимать в этом случае равнодействующую всех сил, действующих на точку.
Вопросы для самопроверки.
1. Дайте определение материальной точки.
2. Сформулируйте законы (аксиомы) динамики.
3. Сформулируйте первую и вторую задачи динамики точки.
4. Какое свойство тела характеризует его масса?
Тема 1.13. Основы кинетостатики.
1.13.1. Принцип 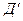 Аламбера .
Аламбера .
1.13.2. Понятие силы инерции.
1.13.1. Принцип, который обычно связывают с именем выдающегося французского ученого Ж.  Аламбера (1717—1783), лежит в основе важного метода динамики, позволяющего задачи динамики формально сводить к задачам статики.
Аламбера (1717—1783), лежит в основе важного метода динамики, позволяющего задачи динамики формально сводить к задачам статики.
 Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила
Допустим, что к несвободной материальной точке М массы т приложена некоторая активная сила 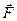 . Освобождая мысленно точку от связей, заменим их действие на точку силой
. Освобождая мысленно точку от связей, заменим их действие на точку силой 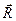 реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы
реакции этих связей. Тогда точку М можно считать свободной, но находящейся под действием силы 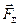 , являющейся равнодействующей сил
, являющейся равнодействующей сил 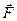 и
и 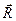 (рис. 1.13.1.). По основному уравнению динамики точки
(рис. 1.13.1.). По основному уравнению динамики точки 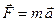 . Условно приложим к точке М еще и вектор
. Условно приложим к точке М еще и вектор 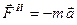 .
.
Вектор 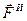 , равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил
, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки, называется силой инерции этой точки. Геометрическая сумма сил
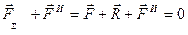
и совокупность сил 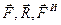 представляет, следовательно, уравновешенную систему.
представляет, следовательно, уравновешенную систему.
Симла 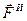 инерции материальной точки условно прилагается к самой материальной точке, и потому получающееся при этом равновесие является не действительным, а лишь условным, воображаемым равновесием.
инерции материальной точки условно прилагается к самой материальной точке, и потому получающееся при этом равновесие является не действительным, а лишь условным, воображаемым равновесием.
Однако такое условное присоединение силы инерции точки к числу сил, в действительности к ней приложенных, позволяет применить к решению задач динамики хорошо известные приемы статики и лежит в основе метода, называемого методом кинетостатики.
Идея метода кинетостатики может быть сформулирована для материальной точки следующим образом: во всякий момент движения материальной точки приложенные к ней активные силы, силы реакций наложенных на нее связей и сила инерции данной точки (условно приложенная к ней самой) взаимно уравновешиваются.
Метод кинетостатики вследствие своей простоты и наглядности широко применяется в технической практике для решения задач динамики. Особенно удобен этот метод для определения так называемых динамических реакций связей, т. е. реакций, возникающих в связях при движении системы. Этим методом можно пользоваться и для определения ускорений тел, входящих в состав системы.
Наряду с этим заметим, что все без исключения задачи динамики можно решать и без применения метода кинетостатики, не пользуясь вовсе понятием сил инерции.
1.13.2. В природе не бывает одностороннего действия сил. Если материальная точка массы т в результате взаимодействия с другими, окружающими ее телами, приобрела некоторое ускорение 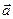 , то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна
, то к этим телам, согласно третьему основному закону механики, приложены со стороны точки силы противодействия. Геометрическая сумма этих сил, приложенных, вообще говоря, к различным телам, формально равна 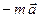 , т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет.
, т.е. равна силе инерции точки. Только формально, так как сложение сил приложенных к различным телам физического смысла не имеет.
Реально существуют лишь составляющие этой силы, приложенные к тем телам, которые являются источником активных сил, действующих на движущуюся с ускорением материальную точку, и к связям, наложенным на точку. О силе инерции 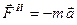 можно говорить как о реальной силе лишь в том случае, когда на точку действует только одно тело.
можно говорить как о реальной силе лишь в том случае, когда на точку действует только одно тело.
Рассмотрим такой пример. Рабочий катит перед собой по рельсам вагонетку, сообщая ей ускорение 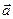 . Для простоты считаем, что вагонетка движется по горизонтальному прямолинейному пути и никаких сопротивлений своему движению не встречает. Следовательно, источником силы, сообщающей вагонетке ускорение
. Для простоты считаем, что вагонетка движется по горизонтальному прямолинейному пути и никаких сопротивлений своему движению не встречает. Следовательно, источником силы, сообщающей вагонетке ускорение 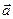 , является только рабочий. По основному закону динамики для сообщения вагонетке этого ускорения рабочий должен приложить к ней силу
, является только рабочий. По основному закону динамики для сообщения вагонетке этого ускорения рабочий должен приложить к ней силу 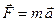 , где т—масса вагонетки. Всякое действие одного тела на другое всегда сопровождается равным и противоположно направленным действием второго тела на первое. Следовательно, рабочий будет встречать со стороны вагонетки силу противодействия
, где т—масса вагонетки. Всякое действие одного тела на другое всегда сопровождается равным и противоположно направленным действием второго тела на первое. Следовательно, рабочий будет встречать со стороны вагонетки силу противодействия 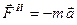 , равную по модулю силе
, равную по модулю силе 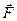 давления рабочего на вагонетку и направленную в противоположную сторону, т. е. в сторону, противоположную ускорению. Очевидно, что сила
давления рабочего на вагонетку и направленную в противоположную сторону, т. е. в сторону, противоположную ускорению. Очевидно, что сила 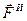 вагонетки приложена не к ней самой, а к руке рабочего (рис. 1.13.2.).
вагонетки приложена не к ней самой, а к руке рабочего (рис. 1.13.2.).
 Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке.
Необходимо всегда иметь в виду, что, применяя метод кинетостатики, мы лишь условно прилагаем силу инерции материальной точки к самой точке.
 В общем случае движения точки по, криволинейной траектории ускорение
В общем случае движения точки по, криволинейной траектории ускорение 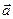 точки , как мы знаем, удобно разлагать на две составляющие: касательное (тангенсальное) ускорение
точки , как мы знаем, удобно разлагать на две составляющие: касательное (тангенсальное) ускорение 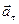 (
( 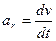 )направленное по касательной к траектории движения, и нормальное ускорение
)направленное по касательной к траектории движения, и нормальное ускорение 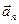 (
( 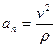 ,
, 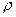 - радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью
- радиус кривизны траектории в данном положении материальной точки), направленное по нормали к центру кривизны траектории. Положим, что к свободной материальной точке М массы т, движущейся со скоростью 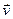 , приложена сила
, приложена сила 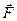 , направление которой образует с направлением скорости
, направление которой образует с направлением скорости 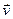 некоторый угол (рис. 1.13.3.). Точка в этом случае будет двигаться по криволинейному пути с ускорением
некоторый угол (рис. 1.13.3.). Точка в этом случае будет двигаться по криволинейному пути с ускорением 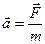 , направленным одинаково с силой
, направленным одинаково с силой 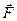 .
.
Очевидно, что при криволинейном движении точки приложенную к ней силу 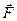 можно разложить на две составляющие: касательную силу
можно разложить на две составляющие: касательную силу 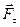 , изменяющую модуль скорости точки, и нормальную силу
, изменяющую модуль скорости точки, и нормальную силу 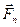 , изменяющую направление скорости точки.
, изменяющую направление скорости точки.
При криволинейном движении точки её силу инерции также можно разложить на две составляющие: касательную силу инерции 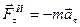 , напрвленную противоположно касательному ускорению точки, и нормальную силу инерции
, напрвленную противоположно касательному ускорению точки, и нормальную силу инерции 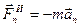 , направленную противоположно нормальному ускорению точки.
, направленную противоположно нормальному ускорению точки.
При несвободном криволинейном движении точки, действующей на неё нормальной силой будет реакция связи, заставляющая точку отклоняться от прямолинейного пути и, следовательно, сообщающая ей соответствующее нормальное ускорение. Силой же, действующей на связь, будет нормальная сила инерции данной точки.
 Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар
Положим, что в криволинейном желобе лежит шар (рис. 1.13.4.). Если сообщить ему толчок в направлении оси желоба, то возникнут одновременно две силы: нормальная реакция стенок желоба на шар 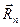 и нормальная сила инерции
и нормальная сила инерции 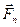 —давление шара на стенки жалоба, направленная по той же нормали от центра. Если желоб взять резиновым, то действие нормальной силы инерции наглядно проявится выпучиванием при движении шара наружной поверхности желоба.
—давление шара на стенки жалоба, направленная по той же нормали от центра. Если желоб взять резиновым, то действие нормальной силы инерции наглядно проявится выпучиванием при движении шара наружной поверхности желоба.
 Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти
Подвешенное к нити тело (рис. 1.13.5.) натягивает ее при покое с силой, равной по модулю силе тяже- сти 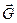 тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой
тела. Будучи же приведено в колебание, тело натягивает нить в момент ее перехода через вертикальное положение с силой 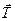 (
( 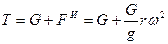 ). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила
). При быстром вращении центробежная сила инерции тела, приложенная к нити, осуществляющей связь, заставляющую тело совершать криволинейное движение, может настолько увеличить натяжение нити, что произойдет ее разрыв. В момент разрыва нити исчезнет реакция связи (сила 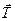 ), приложенная к телу, так как исчезает связь, делавшая его движение несвободным; в тот же самый момент исчезнет и нормальная сила инерции, и тело будет перемещаться по касательной к окружности в той ее точке, в которой оно находилось в момент разрыва нити.
), приложенная к телу, так как исчезает связь, делавшая его движение несвободным; в тот же самый момент исчезнет и нормальная сила инерции, и тело будет перемещаться по касательной к окружности в той ее точке, в которой оно находилось в момент разрыва нити.
Аналогичным действием нормальной силы инерции объясняется и происходящий иногда разрыв маховиков при их очень быстром вращении. Если вся масса вращающегося тела распределена симметрично относительно его оси вращения, то нормальные силы инерции, развиваемые отдельными его частями, сказываются только в возникновении динамических напряжений (внутренних усилий) в материале тела. Эти динамические напряжения при больших скоростях могут достигать весьма больших значений, и с ними безусловно нужно считаться. Но если масса вращающегося тела распределена несимметрично относительно оси вращения, то нормальные силы инерции отдельных частиц тела оказывают также еще и добавочное давление на подшипники, увеличивая трение в подшипниках и их износ. Вследствие вращения тела равнодействующая неуравновешенных сил инерции все время изменяет свое направление, а это ведет к нежелательной вибрации тела. Вопрос об уравновешивании сил инерции имеет большое значение в современном машиностроении и рассматривается в теории механизмов и машин. При проектировании каждой новой машины необходимо учитывать силы инерции, которые могут возникнуть в ней при различных условиях работы.
Вопросы для самопроверки.
1. Что называется силой инерции точки?
2. Сформулируйте принцип 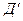 Аламбера.
Аламбера.
Дата добавления: 2015-09-02; просмотров: 1878;